
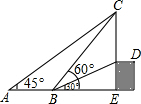
 如图,从点A看一高台上的电线杆CD,顶端C的仰角为45°,向前走6米到B点,测得其顶端C和杆底D的仰角分别是60°和30°,求电线杆CD的高(精确到0.1米).
如图,从点A看一高台上的电线杆CD,顶端C的仰角为45°,向前走6米到B点,测得其顶端C和杆底D的仰角分别是60°和30°,求电线杆CD的高(精确到0.1米).
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| 3 |
| 3 |
| ||
| 3 |
| ||
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
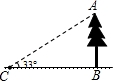 (Ⅰ)如图,从点C测得树的顶端的仰角为33°,BC=20米,则树高AB=
(Ⅰ)如图,从点C测得树的顶端的仰角为33°,BC=20米,则树高AB=查看答案和解析>>
科目:初中数学 来源: 题型:
 探照灯、锅形天线、汽车灯以及其他很多灯具都与抛物线形状有关.如图,从点O照射到抛物线上的光线OB,OC等反射以后沿着与POQ平行的方向射出.图中如果∠BOP=45°,∠QOC=88°,那么∠ABO和∠DCO各是多少度?
探照灯、锅形天线、汽车灯以及其他很多灯具都与抛物线形状有关.如图,从点O照射到抛物线上的光线OB,OC等反射以后沿着与POQ平行的方向射出.图中如果∠BOP=45°,∠QOC=88°,那么∠ABO和∠DCO各是多少度?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
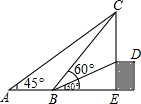 如图,从点A看一高台上的电线杆CD,顶端C的仰角为45°,向前走6米到B点,测得其顶端C和杆底D的仰角分别是60°和30°,求电线杆CD的高(精确到0.1米).
如图,从点A看一高台上的电线杆CD,顶端C的仰角为45°,向前走6米到B点,测得其顶端C和杆底D的仰角分别是60°和30°,求电线杆CD的高(精确到0.1米).查看答案和解析>>
科目:初中数学 来源:2011-2012学年浙江省绍兴市嵊州市城关中学九年级(下)第二次月考数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com