
”¾ĢāÄæ”æÖŠĒļ¼Ń½ŚŹ±£¬ĪŅ¹śÓŠÉĶŌĀŗĶ³ŌŌĀ±żµÄ“«Ķ³£¬Ä³Š£ŹżŃ§ŠĖȤŠ”×éĪŖĮĖĮĖ½ā±¾Š£Ń§ÉśĻ²°®ŌĀ±żµÄĒéæö£¬Ė껜³éČ”ĮĖ60ĆūĶ¬Ń§½ųŠŠĪŹ¾ķµ÷²é£¬¾¹żĶ³¼Ęŗó»ęÖĘĮĖĮ½·łÉŠ²»ĶźÕūµÄĶ³¼ĘĶ¼£®

£Ø×¢£ŗ²ĪÓėĪŹ¾ķµ÷²éµÄĆæŅ»Ī»Ķ¬Ń§ŌŚČĪŗĪŅ»ÖÖ·ÖĄąĶ³¼ĘÖŠÖ»ÓŠŅ»ÖÖŃ”Ōń£©
Ēėøł¾ŻĶ³¼ĘĶ¼Ķź³ÉĻĀĮŠĪŹĢā£ŗ
£Ø1£©ÉČŠĪĶ³¼ĘĶ¼ÖŠ£¬”°ŗÜĻ²»¶”±µÄ²æ·ÖĖł¶ŌÓ¦µÄŌ²ŠÄ½ĒĪŖ__________¶Č£»ĢõŠĪĶ³¼ĘĶ¼ÖŠ£¬ŗÜĻ²»¶”°¶¹É³”±ŌĀ±żµÄѧɜӊ__________ČĖ£»
£Ø2£©ČōøĆŠ£¹²ÓŠŃ§Éś900ČĖ£¬Ēėøł¾ŻÉĻŹöµ÷²é½į¹ū£¬¹Ą¼ĘøĆŠ£Ń§ÉśÖŠ”°ŗÜĻ²»¶”±ŗĶ”°±Č½ĻĻ²»¶”±ŌĀ±żµÄ¹²ÓŠ__________ČĖ£®
£Ø3£©¼×Ķ¬Ń§×ī°®³ŌŌĘĶČŌĀ±ż£¬ŅŅĶ¬Ń§×ī°®³Ō¶¹É³ŌĀ±ż£¬ĻÖÓŠÖŲĮ攢°ü×°ĶźČ«Ņ»ŃłµÄŌĘĶČ”¢¶¹É³”¢Į«ČŲ”¢µ°»ĘĖÄÖÖŌĀ±żø÷Ņ»øö£¬ČĆ¼×”¢ŅŅĆæČĖø÷Ń”Ņ»øö£¬ĒėÓĆ»Ź÷דĶ¼·Ø»ņĮŠ±ķ·Ø£¬Ēó³ö¼×”¢ŅŅĮ½ČĖÖŠÓŠĒŅÖ»ÓŠŅ»ČĖє֊×Ō¼ŗ×ī°®³ŌµÄŌĀ±żµÄøÅĀŹ£®
”¾“š°ø”æ£Ø1£©126”ć£¬4£Ø2£©675£Ø3£©![]()
”¾½āĪö”æ
£Ø1£©øł¾Ż”°ŗÜĻ²»¶”±µÄ²æ·ÖÕ¼µÄ°Ł·Ö±Č£¬¼ĘĖćĖł¶ŌÓ¦µÄŌ²ŠÄ½Ē£»
£Ø2£©ÓĆŃł±¾¹Ą¼Ę×ÜĢåµÄĖ¼Ļė¼“æɽā¾öĪŹĢā£®
£Ø3£©»³öŹ÷דĶ¼£¬øł¾ŻøÅĀŹµÄ¶ØŅ弓æɽā¾ö£®
½ā£ŗ£Ø1£©”ß”°ŗÜĻ²»¶”±µÄ²æ·ÖÕ¼µÄ°Ł·Ö±ČĪŖ£ŗ1©25%©40%=35%£¬
”ąÉČŠĪĶ³¼ĘĶ¼ÖŠ£¬”°ŗÜĻ²»¶”±µÄ²æ·ÖĖł¶ŌÓ¦µÄŌ²ŠÄ½ĒĪŖ£ŗ360”ć”Į35%=126”ć£»
”ß”°ŗÜĻ²»¶”±ŌĀ±żµÄĶ¬Ń§Źż£ŗ60”Į35%=21£ØČĖ£©£¬
”ąĢõŠĪĶ³¼ĘĶ¼ÖŠ£¬Ļ²»¶”°¶¹É³”±ŌĀ±żµÄѧɜŹż£ŗ21©6©3©8=4£ØČĖ£©£¬
¹Ź“š°ø·Ö±šĪŖ126”ć£¬4£®
£Ø2£©900Ćūѧɜ֊”°ŗÜĻ²»¶”±µÄÓŠ900”Į35%=315ČĖ£¬900Ćūѧɜ֊”°±Č½ĻĻ²»¶”±µÄÓŠ900”Į40%=360ČĖ£¬
”ą¹Ą¼ĘøĆŠ£Ń§ÉśÖŠ”°ŗÜĻ²»¶”±ŗĶ”°±Č½ĻĻ²»¶”±ŌĀ±żµÄ¹²ÓŠ675ČĖ£®
¹Ź“š°øĪŖ675£®
£Ø3£©ĪŖĮĖ±ķŹ¾·½±ć£¬¼ĒŌĘĶČ”¢¶¹É³”¢Į«ČŲ”¢µ°»ĘĖÄÖÖŌĀ±ż·Ö±šĪŖA”¢B”¢C”¢D£®»³öµÄŹ÷דĶ¼ČēĶ¼ĖłŹ¾£¬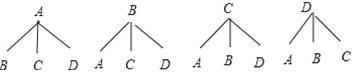
”ą¼×”¢ŅŅĮ½ČĖÖŠÓŠĒŅÖ»ÓŠŅ»ČĖє֊×Ō¼ŗ×ī°®³ŌµÄŌĀ±żµÄøÅĀŹ=![]() =
=![]()



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ½ā²»µČŹ½×é£ŗ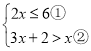 Ēė½įŗĻĢāŅāĢīæÕ£¬Ķź³É±¾ĢāµÄ½ā“š£ŗ
Ēė½įŗĻĢāŅāĢīæÕ£¬Ķź³É±¾ĢāµÄ½ā“š£ŗ
£Ø1£©½ā²»µČŹ½¢Ł£¬µĆ£ŗ””””£»
£Ø2£©½ā²»µČŹ½¢ŚµĆ£ŗ””””£»
£Ø3£©°Ń²»µČŹ½¢ŁŗĶ¢ŚµÄ½ā¼ÆŌŚŹżÖįÉĻ±ķŹ¾³öĄ“£»
![]()
£Ø4£©Ō²»µČŹ½×éµÄ½ā¼ÆĪŖ£ŗ””””£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖ³«µ¼½”æµ»·±££¬×Ō“ųĖ®±ŅŃ³ÉĪŖŅ»ÖÖŗĆĻ°¹ß£¬Ä³³¬ŹŠĻśŹŪ¼×£¬ŅŅĮ½ÖÖŠĶŗÅĖ®±£¬½ų¼ŪŗĶŹŪ¼Ū¾ł±£³Ö²»±ä£¬ĘäÖŠ¼×ÖÖŠĶŗÅĖ®±½ų¼ŪĪŖ25ŌŖ/øö£¬ŅŅÖÖŠĶŗÅĖ®±½ų¼ŪĪŖ45ŌŖ/øö£¬ĻĀ±ķŹĒĒ°Į½ŌĀĮ½ÖÖŠĶŗÅĖ®±µÄĻśŹŪĒéæö£ŗ
Ź±¼ä | ĻśŹŪŹżĮæ£Øøö£© | ĻśŹŪŹÕČė£ØŌŖ£©£ØĻśŹŪŹÕČė£½ŹŪ¼Ū”ĮĻśŹŪŹżĮ棩 | |
¼×ÖÖŠĶŗÅ | ŅŅÖÖŠĶŗÅ | ||
µŚŅ»ŌĀ | 22 | 8 | 1100 |
µŚ¶žŌĀ | 38 | 24 | 2460 |
£Ø1£©Ēó¼×”¢ŅŅĮ½ÖÖŠĶŗÅĖ®±µÄŹŪ¼Ū£»
£Ø2£©µŚČżŌĀ³¬ŹŠ¼Ę»®ŌŁ¹ŗ½ų¼×”¢ŅŅĮ½ÖÖŠĶŗÅĖ®±¹²80øö£¬ÕāÅśĖ®±½ų»õµÄŌ¤Ėć³É±¾²»³¬¹ż2600ŌŖ£¬ĒŅ¼×ÖÖŠĶŗÅĖ®±×ī¶ą¹ŗ½ų55øö£¬ŌŚ80øöĖ®±Č«²æŹŪĶźµÄĒéæöĻĀÉč¹ŗ½ų¼×ÖÖŗÅĖ®±aøö£¬ĄūČóĪŖwŌŖ£¬Š“³öwÓėaµÄŗÆŹż¹ŲĻµŹ½£¬²¢Ēó³öµŚČżŌĀµÄ×ī“óĄūČó£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻßy=©x2+bx+cŗĶÖ±Ļßy=x+1½»ÓŚA£¬BĮ½µć£¬µćAŌŚxÖįÉĻ£¬µćBŌŚÖ±Ļßx=3ÉĻ£¬Ö±Ļßx=3ÓėxÖį½»ÓŚµćC
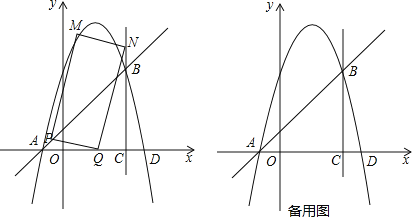
£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©µćP“ÓµćA³ö·¢£¬ŅŌĆæĆė![]() øöµ„Ī»³¤¶ČµÄĖŁ¶ČŃŲĻ߶ĪABĻņµćBŌĖ¶Æ£¬µćQ“ÓµćC³ö·¢£¬ŅŌĆæĆė2øöµ„Ī»³¤¶ČµÄĖŁ¶ČŃŲĻ߶ĪCAĻņµćAŌĖ¶Æ£¬µćP£¬QĶ¬Ź±³ö·¢£¬µ±ĘäÖŠŅ»µćµ½“ļÖÕµćŹ±£¬ĮķŅ»øöµćŅ²ĖęÖ®Ķ£Ö¹ŌĖ¶Æ£¬ÉčŌĖ¶ÆŹ±¼äĪŖtĆė£Øt£¾0£©£®ŅŌPQĪŖ±ß×÷¾ŲŠĪPQNM£¬Ź¹µćNŌŚÖ±Ļßx=3ÉĻ£®
øöµ„Ī»³¤¶ČµÄĖŁ¶ČŃŲĻ߶ĪABĻņµćBŌĖ¶Æ£¬µćQ“ÓµćC³ö·¢£¬ŅŌĆæĆė2øöµ„Ī»³¤¶ČµÄĖŁ¶ČŃŲĻ߶ĪCAĻņµćAŌĖ¶Æ£¬µćP£¬QĶ¬Ź±³ö·¢£¬µ±ĘäÖŠŅ»µćµ½“ļÖÕµćŹ±£¬ĮķŅ»øöµćŅ²ĖęÖ®Ķ£Ö¹ŌĖ¶Æ£¬ÉčŌĖ¶ÆŹ±¼äĪŖtĆė£Øt£¾0£©£®ŅŌPQĪŖ±ß×÷¾ŲŠĪPQNM£¬Ź¹µćNŌŚÖ±Ļßx=3ÉĻ£®
¢Łµ±tĪŖŗĪÖµŹ±£¬¾ŲŠĪPQNMµÄĆ껿×īŠ”£æ²¢Ēó³ö×īŠ”Ć껿£»
¢ŚÖ±½ÓŠ“³öµ±tĪŖŗĪÖµŹ±£¬Ē”ŗĆÓŠ¾ŲŠĪPQNMµÄ¶„µćĀäŌŚÅ×ĪļĻßÉĻ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
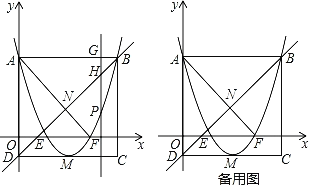
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻßy£½x2+bx+c¾¹żA £Ø0£¬3£©£¬B £Ø4£¬3£©Į½µć£¬ÓėxÖį½»ÓŚµćE£¬F£¬ŅŌABĪŖ±ß×÷¾ŲŠĪABCD£¬ĘäÖŠCD±ß¾¹żÅ×ĪļĻßµÄĻīµćM£¬µćPŹĒÅ×ĪļĻßÉĻŅ»¶Æµć£ØµćP²»ÓėµćA£¬BÖŲŗĻ£©£¬¹żµćP×÷yÖįµÄĘ½ŠŠĻß1ÓėÖ±ĻßAB½»ÓŚµćG£¬ÓėÖ±ĻßBD½»ÓŚµćH£¬Į¬½ÓAF½»Ö±ĻßBDÓŚµćN£®
£Ø1£©ĒóøĆÅ×ĪļĻߵĽāĪöŹ½ŅŌ¼°¶„µćMµÄ×ų±ź£»
£Ø2£©µ±Ļ߶ĪPH£½2GHŹ±£¬ĒóµćPµÄ×ų±ź£»
£Ø3£©ŌŚÅ×ĪļĻßÉĻŹĒ·ń“ęŌŚµćP£¬Ź¹µĆŅŌµćP£¬E£¬N£¬FĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪ£æČō“ęŌŚ£¬ĒėĒó³öµćPµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ¾ŲŠĪABCDÖŠ£¬EŹĒABÉĻŅ»µć£¬½«”÷ADEŃŲDE·ÕŪ£¬µćAĒ”ŗĆĀäŌŚBCÉĻ£¬¼ĒĪŖA1£¬ÕŪŗŪĪŖDE£®ŌŁ½«”ĻBŃŲEA1ĻņÄŚ·ÕŪ£¬µćBĒ”ŗĆĀäŌŚDEÉĻ£¬¼ĒĪŖB1£®ČōAD£½1£¬ŌņABµÄ³¤ĪŖ_____£®
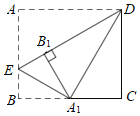
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚRt”÷ABCÖŠ£¬”ĻC£½90”ć£¬AC£½8£¬BC£½6£®¶ÆµćP“ÓµćA³ö·¢£¬ŃŲABŅŌĆæĆė5øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņÖÕµćBŌĖ¶Æ£®µ±µćP²»ÓėµćAÖŲŗĻŹ±£¬¹żµćP×÷PD”ĶACÓŚµćD”¢PE”ĪAC£¬¹żµćD×÷DE”ĪAB£¬DEÓėPE½»ÓŚµćE£®ÉčµćPµÄŌĖ¶ÆŹ±¼äĪŖtĆė£®
£Ø1£©Ļ߶ĪADµÄ³¤ĪŖ”” ””£®£ØÓĆŗ¬tµÄ“śŹżŹ½±ķŹ¾£©£®
£Ø2£©µ±µćEĀäŌŚBC±ßÉĻŹ±£¬ĒótµÄÖµ£®
£Ø3£©Éč”÷DPEÓė”÷ABCÖŲµž²æ·ÖĶ¼ŠĪµÄĆ껿ĪŖS£¬ĒóSÓėtÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£®
£Ø4£©ČōĻ߶ĪPEµÄÖŠµćĪŖQ£¬µ±µćQĀäŌŚ”÷ABCŅ»±ß“¹Ö±Ę½·ÖĻßÉĻŹ±£¬Ö±½ÓŠ“³ötµÄÖµ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB=AC£¬ŅŌABĪŖÖ±¾¶µÄ°ėŌ²½»ACÓŚµćD£¬½»BCÓŚµćE£¬ŃÓ³¤AEÖĮµćF£¬Ź¹EF=AE£¬Į¬½ÓFB”¢FC£®
£Ø1£©ĒóÖ¤£ŗĖıߊĪABFCŹĒĮāŠĪ£»
£Ø2£©ČōAD=![]() £¬BE=1£¬Ēó°ėŌ²µÄĆ껿£®
£¬BE=1£¬Ēó°ėŌ²µÄĆ껿£®
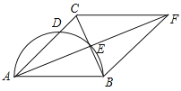
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ”ŃAÓėĮāŠĪABCDµÄ±ßBCĻąĒŠÓŚµćE£¬Óė±ßABĻą½»ÓŚµćF£¬Į¬½ÓEF£®
£Ø1£©ĒóÖ¤£ŗCDŹĒ”ŃAµÄĒŠĻߣ»
£Ø2£©Čō”ŃAµÄ°ė¾¶ĪŖ2£¬tan”ĻBEF£½![]() £¬ĒóĶ¼ÖŠŅõÓ°²æ·ÖµÄĆ껿£®
£¬ĒóĶ¼ÖŠŅõÓ°²æ·ÖµÄĆ껿£®
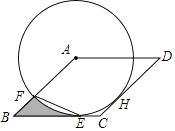
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com