
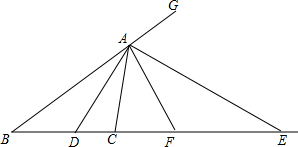
 如图,已知△ABC中,AD,AE分别是∠CAB及其外角平分线,分别交CB及CB的延长线于D、E,F为DE的中点,求证:
如图,已知△ABC中,AD,AE分别是∠CAB及其外角平分线,分别交CB及CB的延长线于D、E,F为DE的中点,求证:分析 (1)如图1,易证∠DAE=90°,然后运用“直角三角形斜边上的中线等于斜边的一半”即可解决问题;
(2)过点B作BM∥AC交AD的延长线于点M,如图2,易证AB=MB.由BM∥AC可得△CDA∽△BDM,则有$\frac{CD}{BD}$=$\frac{AC}{MB}$,由AB=MB可得$\frac{CD}{BD}$=$\frac{AC}{AB}$;
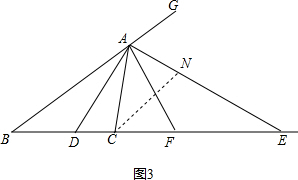
(3)过点C作CN∥AB交AE于点N,如图3,易证CA=CN.由CN∥AB可得△ECN∽△EBA,则有$\frac{CE}{BE}$=$\frac{CN}{BA}$,由CA=CN可得$\frac{CE}{BE}$=$\frac{AC}{AB}$;
(4)由(2)、(3)中的结论可得$\frac{CD}{BD}$=$\frac{AC}{AB}$=$\frac{CE}{BE}$,即CD•BE=BD•CE.
解答  证明:(1)∵AD平分∠BAC,AE平分∠GAC,
证明:(1)∵AD平分∠BAC,AE平分∠GAC,
∴∠BAD=∠DAC=$\frac{1}{2}$∠BAC,∠GAE=∠CAE=$\frac{1}{2}$∠GAC,
∴∠DAE=∠DAC+∠CAE=$\frac{1}{2}$∠BAC+$\frac{1}{2}$∠GAC=$\frac{1}{2}$×180°=90°.
∵F为DE的中点,
∴AF=DF=FE;
(2)过点B作BM∥AC交AD的延长线于点M,如图2,
则有∠M=∠DAC.
∵∠BAD=∠DAC,
∴∠M=∠BAD,
∴AB=MB.
∵BM∥AC,
∴△CDA∽△BDM,
∴$\frac{CD}{BD}$=$\frac{AC}{MB}$,
∴$\frac{CD}{BD}$=$\frac{AC}{AB}$;
(3)过点C作CN∥AB交AE于点N,如图3,
则有∠GAE=∠ANC.
∵∠GAE=∠CAE,
∴ ∠ANC=∠CAE,
∠ANC=∠CAE,
∴CA=CN.
∵CN∥AB,
∴△ECN∽△EBA,
∴$\frac{CE}{BE}$=$\frac{CN}{BA}$,
∴$\frac{CE}{BE}$=$\frac{AC}{AB}$;
(4)由(2)得$\frac{CD}{BD}$=$\frac{AC}{AB}$,
由(3)得$\frac{CE}{BE}$=$\frac{AC}{AB}$,
∴$\frac{CD}{BD}$=$\frac{CE}{BE}$,
∴CD•BE=BD•CE.
点评 本题主要考查了相似三角形的判定与性质、直角三角形斜边上的中线等于斜边的一半、等腰三角形的判定、角平分线的定义、平角的定义等知识,添加平行线是构造相似三角形常用的一种方法,应熟练掌握.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{13}+\sqrt{3}=\sqrt{16}=4$ | B. | $\sqrt{121÷4}=\sqrt{121}÷\sqrt{4}=\frac{11}{2}$ | C. | $3+\sqrt{3}=3\sqrt{3}$ | D. | $\sqrt{4\frac{1}{3}}=2\sqrt{\frac{1}{3}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 打开电视机,正在播广告,是必然事件 | |
| B. | 在连续5次的数学测试中,两名同学的平均分相同,方差较大的同学数学成绩更稳定 | |
| C. | 某同学连续10次抛掷质量均匀的硬币,3次正面向上,因此正面向上的概率是30% | |
| D. | 从一个只装有白球的缸里摸出一个球,摸出的球是白球 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
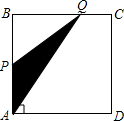 如图,四边形ABCD是矩形,AB=8,BC=4,动点P以每秒2个单位的速度从点A沿线段AB向B点运动,同时动点Q以每秒3个单位的速度从点B出发沿B-C-D的方向运动,当点Q到达点D时P、Q同时停止运动,若记△PQA的面积为y,运动时间为x,则下列图象中能大致表示y与x之间函数关系图象的是( )
如图,四边形ABCD是矩形,AB=8,BC=4,动点P以每秒2个单位的速度从点A沿线段AB向B点运动,同时动点Q以每秒3个单位的速度从点B出发沿B-C-D的方向运动,当点Q到达点D时P、Q同时停止运动,若记△PQA的面积为y,运动时间为x,则下列图象中能大致表示y与x之间函数关系图象的是( )| A. | 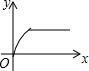 | B. | 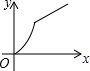 | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图:在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是( )
如图:在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是( )| A. | 矩形 | B. | 菱形 | C. | 正方形 | D. | 任意四边形 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=-1,下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=-1,下列结论:| A. | ①② | B. | 只有① | C. | ③④ | D. | ①④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com