
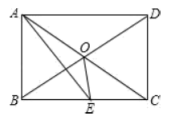
【题目】如图所示,矩形ABCD中,AE平分![]() 交BC于E,
交BC于E,![]() ,则下面的结论:①
,则下面的结论:①![]() 是等边三角形;②
是等边三角形;②![]() ;③
;③![]() ;④
;④![]() ,其中正确结论有( )
,其中正确结论有( )
A. 1个B. 2个C. 3个D. 4个
【答案】C
【解析】
根据矩形性质求出OD=OC,根据角求出 ∠DOC = 60°即可得出三角形DOC是等边三角形,求出AC= 2AB, 即可判断②,求出∠BOE= 75°,∠AOB = 60相加即可求出,∠AOE根据等底等高的三角形面积相等得出![]() .
.
∵四边形ABCD是矩形,
∴∠BAD=90°,OA=OC,OD=OB,AC=BD
∴OA=OD=OC=OB
∵AE平分∠BAD,
∴∠DAE=15°.
∴∠CAE=15°,
∴∠DAC=30°.
∵OA=OD,
∴∠ODA=∠DAC=30°.
∴∠DOC=60°.
∵OD=OC,
∴△ODC是等边三角形.
∴①正确;
∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°.
∴∠DAC=∠ACB=30°.
∴AC=2AB.
∵AC>BC,
∴2AB>BC.
∴②错误;
∵AD∥BC,
∴∠DBC=∠ADB=30°.
∵AE平分∠DAB,∠DAB=90°,
∴∠DAE=∠BAE=45°.
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠AEB=∠BAE,
∴AB=BE.
∴四边形ABCD是矩形.
∴∠DOC=60°,DC=AB,
∵△DOC是等边三角形,
∴DC=OD.
∴BE=BO.
∴∠BOE=75°,
∵∠AOB=∠DOC=60°,
∴∠AOE=135°.
∴③正确;
∵OA=OC,
∴根据等底等高的三角形面积相等可知S△AOE=S△COE
∴④正确
故正确答案是C.


科目:初中数学 来源: 题型:
【题目】已知a,b为有理数,且a,b不为0,则定义有理数对(a,b)的“真诚值”为d(a,b)= ,如有理数对(3,2)的“真诚值”为d(3,2)=23﹣10=﹣2,有理数对(﹣2,5)的“真诚值”为d(﹣2,5)=(﹣2)5﹣10=﹣42.
,如有理数对(3,2)的“真诚值”为d(3,2)=23﹣10=﹣2,有理数对(﹣2,5)的“真诚值”为d(﹣2,5)=(﹣2)5﹣10=﹣42.
(1)求有理数对(﹣3,2)与(1,2)的“真诚值”;
(2)求证:有理数对(a,b)与(b,a)的“真诚值”相等;
(3)若(a,2)的“真诚值”的绝对值为|d(a,2)|,若|d(a,2)|=6,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
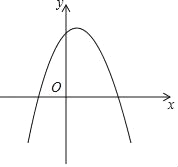
【题目】在平面直角坐标系中,规定:抛物线y=a(x﹣h)2+k的关联直线为y=a(x﹣h)+k.
例如:抛物线y=2(x+1)2﹣3的关联直线为y=2(x+1)﹣3,即y=2x﹣1.
(1)如图,对于抛物线y=﹣(x﹣1)2+3.
①该抛物线的顶点坐标为_____,关联直线为_____,该抛物线与其关联直线的交点坐标为_____和_____;
②点P是抛物线y=﹣(x﹣1)2+3上一点,过点P的直线PQ垂直于x轴,交抛物线y=﹣(x﹣1)2+3的关联直线于点Q.设点P的横坐标为m,线段PQ的长度为d(d>0),求当d随m的增大而减小时,d与m之间的函数关系式,并写出自变量m的取值范围.
(2)顶点在第一象限的抛物线y=﹣a(x﹣1)2+4a与其关联直线交于点A,B(点A在点B的左侧),与x轴负半轴交于点C,直线AB与x轴交于点D,连结AC、BC.
①求△BCD的面积(用含a的代数式表示).
②当△ABC为钝角三角形时,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用1块A型钢板可制成2个C型模具和1个D型模具;用1块B型钢板可制成1个C型模具和3个D型模具,现准备A、B型钢板共100块,并全部加工成C、D型模具.
(1)若B型钢板的数量是A型钢板的数量的两倍还多10块,求A、B型钢板各有多少块?
(2)若销售C、D型模具的利润分别为80元/块、100元/块,且全部售出.
①当A型钢板数量为25块时,那么共可制成C型模具 个,D型模具 个;
②当C、D型模具全部售出所得的利润为34400元,求A型钢板有多少块?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四川汶川大地震牵动了三百多万滨州人民的心,全市广大中学生纷纷伸出了援助之手,为抗震救灾踊跃捐款。滨州市振兴中学某班的学生对本校学生自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据。下图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3:4:5:8:6,又知此次调查中捐款25元和30元的学生一共42人。
(1)他们一共调查了多少人?
(2)这组数据的众数、中位数各是多少?
(3)若该校共有1560名学生,估计全校学生捐款多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:

(1)参加比赛有_____名运动员,图①中a的值是_____,补全条形统计图.
(2)统计的这组初赛成绩数据的众数是_____,中位数是_____,平均数是_____.
(3)根据这组初赛成绩,由高到低确定9人进入复赛,请直接写出初赛成绩为1.65m的运动员能否进入复赛.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程
(1)(x﹣5)2=16(直接开平方法) (2)x2﹣4x+1=0(配方法)
(3)x2+3x﹣4=0(公式法) (4)x2+5x﹣3=0(配方法)
查看答案和解析>>
科目:初中数学 来源: 题型:
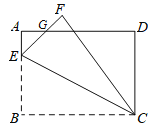
【题目】如图,矩形ABCD中,AB=4,BC=6,E为AB上一点,将△BCE沿CE翻折至△FCE,EF与AD相交于点G,且AG=FG,则线段AE的长为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com