
【题目】如图,锐角△ABC内接于⊙O,若⊙O的半径为6,sinA=![]() ,求BC的长.
,求BC的长.

【答案】BC=8.
【解析】试题分析:通过作辅助线构成直角三角形,再利用三角函数知识进行求解.
试题解析:作⊙O的直径CD,连接BD,则CD=2×6=12.
∵![]()
∴![]()
∴![]()

点睛:直径所对的圆周角是直角.
【题型】解答题
【结束】
22
【题目】如图,一次函数y=k1x+b与反比例函数y=![]() 的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.
的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式k1x+b>![]() 的解集;
的解集;
(3)若P(p,y1),Q(﹣2,y2)是函数y=![]() 图象上的两点,且y1≥y2,求实数p的取值范围.
图象上的两点,且y1≥y2,求实数p的取值范围.

【答案】(1)反比例函数的解析式是y=![]() ;一次函数的解析式是y=x+1;(2)﹣3<x<0或x>2;(3)p≤﹣2或p>0.
;一次函数的解析式是y=x+1;(2)﹣3<x<0或x>2;(3)p≤﹣2或p>0.
;
【解析】试题分析:(1)把A(2,m),B(n,2)代入反比例函数解析式求出m=n, 过A作AE⊥x轴于E,过B作BF⊥y轴于F,延长AE、BF交于D,根据三角形的面积公式可得出关于n的方程,求出n的值,得出![]() 的坐标,代入反比例函数和一次函数的解析式,即可求出答案;
的坐标,代入反比例函数和一次函数的解析式,即可求出答案;
(2)根据![]() 的横坐标,结合图象即可得出答案;
的横坐标,结合图象即可得出答案;
(3)分为两种情况:当点![]() 在第三象限时和当点
在第三象限时和当点![]() 在第一象限时,根据坐标和图象即可得出答案.
在第一象限时,根据坐标和图象即可得出答案.
试题解析:(1)把A(2,m),B(n,2)代入![]() 得:k2=2m=2n,
得:k2=2m=2n,
即m=n,
则A(2,n),
过A作AE⊥x轴于E,过B作BF⊥y轴于F,延长AE、BF交于D,

∵A(2,n),B(n,2),
∴BD=2n,AD=n+2,BC=|2|=2,
∵![]()
![]() 解得:n=3,
解得:n=3,
即A(2,3),B(3,2),
把A(2,3)代入![]() 得:
得:![]()
即反比例函数的解析式是![]()
把A(2,3),B(3,2)代入![]() 得:
得:![]()
解得:![]()
即一次函数的解析式是y=x+1;
(2)∵A(2,3),B(3,2),
∴不等式![]() 的解集是3<x<0或x>2;
的解集是3<x<0或x>2;
(3)分为两种情况:当点P在第三象限时,要使![]() ,实数p的取值范围是
,实数p的取值范围是![]() ,
,
当点P在第一象限时,![]() ,实数p的取值范围是P>0,
,实数p的取值范围是P>0,
即P的取值范围是![]() 或p>0.
或p>0.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
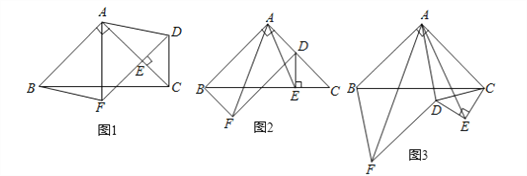
【题目】如图1,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合).在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)求证:△AEF是等腰直角三角形;
(2)如图2,将△CED绕点C逆时针旋转,当点E在线段BC上时,连接AE,求证:AF=![]() AE;
AE;
(3)如图3,将△CED绕点C继续逆时针旋转,当平行四边形ABFD为菱形,且△CED在△ABC的下方时,若AB=2![]() ,CE=2,求线段AE的长.
,CE=2,求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,四边形OABC是长方形,O为原点,点A在x轴上,点C在y轴上且A(10,0),C(0,6),点D在AB边上,将△CBD沿CD翻折,点B恰好落在OA边上点E处.
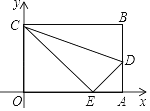
(1)求点E的坐标;
(2)求折痕CD所在直线的函数表达式;
(3)请你延长直线CD交x轴于点F. ①求△COF的面积;
②在x轴上是否存在点P,使S△OCP=![]() S△COF?若存在,求出点P的坐标;若不存在,请说明理由.
S△COF?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,a、b、c 均为非零实数,且 a>b>c,关于 x 的一元二次方程ax2 bx c 0 有两个实数根 x1和 2。(1)4a +2b +c _____0,a _____0,c _________0(填“>”,“=”,“<”)(2)方程 ax2 bx c 0 的另一个根 x1=_______(用含 a、c 的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
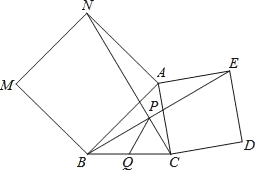
【题目】如图,分别以△ABC的两边AB和AC为边向外作正方形ANMB和正方形ACDE,NC、BE交于点P.
探究:试判断BE和CN的位置关系和数量关系,并说明理由.
应用:Q是线段BC的中点,若BC=6,则PQ= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料一:一个正整数x能写成x=a2﹣b2(a,b均为正整数,且a≠b),则称x为“雪松数”,a,b为x的一个平方差分解,在x的所有平方差分解中,若a2+b2最大,则称a,b为x的最佳平方差分解,此时F(x)=a2+b2.
例如:24=72﹣52,24为雪松数,7和5为24的一个平方差分解,32=92﹣72,32=62﹣22,因为92+72>62+22,所以9和7为32的最佳平方差分解,F(32)=92+72
材料二:若一个四位正整数,它的千位数字与个位数字相同,百位数字与十位数字相同,但四个数字不全相同,则称这个四位数为“南麓数”.例如4334,5665均为“南麓数”.
根据材料回答:
(1)请直接写出两个雪松数,并分别写出它们的一对平方差分解;
(2)试证明10不是雪松数;
(3)若一个数t既是“雪松数”又是“南麓数”,并且另一个“南麓数”的前两位数字组成的两位数与后两位数字组成的两位数恰好是t的一个平方差分解,请求出所有满足条件的数t中F(t)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
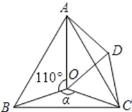
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)试说明:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当∠BOC为多少度时,△AOD是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校初一(2)班组织学生从A地到B地步行野营,匀速前进,该班师生共56人,每8人排成一排,相邻两排之间间隔1米,途中经过一座桥CD,队伍从开始上桥到刚好完全离开桥共用了150秒,当队尾刚好走到桥的一端D处时,排在队尾的游班长发现小蒋还在桥的另一端C处拍照,于是以队伍1.5倍的速度返回去找小萍,同时队伍仍按原速度继续前行,30秒后,小蒋发现游班长返回来找他,便立刻以2.1米/秒的速度向游班长方向行进,小蒋行进40秒后与游班长相遇,相遇后两人以队伍2倍的速度前行追赶队伍.
(1)初一(2)班的队伍长度为 米;
(2)求班级队伍行进的速度(列一元一次方程解决问题);
(3)请问:游班长从D处返回赵小萍开始到他们两人追上队首的刘老师一共用了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
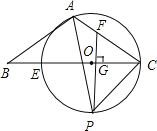
【题目】如图,在△ABC 中,AB=AC,∠BAC=120°,E 为 BC 上一点,以 CE 为直径作⊙O 恰好经过 A、C 两点, PF⊥BC 交 BC 于点 G,交 AC 于点 F.
(1)求证:AB 是⊙O 的切线;
(2)如果 CF =2,CP =3,求⊙O 的直径 EC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com