
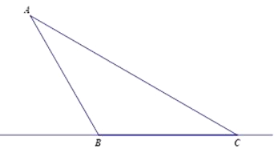
【题目】为保证车辆行驶安全,现在公路旁设立一检测点A观测行驶的汽车是否超速.如图,检测点A到公路的距离是24米,在公路上取两点B、C,使得∠ACB=30°,∠ABC=120°.
(1)求BC的长(结果保留根号);
(2)已知该路段限速为45千米/小时,若测得某汽车从B到C用时2秒,这辆汽车是否超速?说明理由.(参考数据:![]() ≈1.7,
≈1.7,![]() ≈1.4)
≈1.4)
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
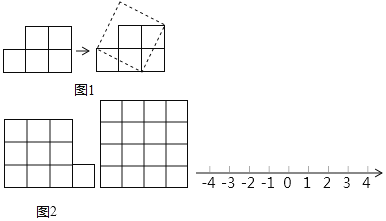
【题目】如图1,有五个边长为1的小正方形组成的图形纸,我们可以把它剪开拼成一个正方形.
(1)拼成的正方形的面积是 ,边长是 .
(2)把10个小正方形组成的图形纸(如图2),剪开并拼成正方形.
①请在4×4方格图内画出这个正方形.
②以小正方形的边长为单位长度画一条数轴,并在数轴上画出表示-![]() 的点.
的点.
(3)这种研究和解决问题的方式,主要体现了 的数学思想方法.
A.数形结合 B.代入 C.换元 D.归纳
查看答案和解析>>
科目:初中数学 来源: 题型:
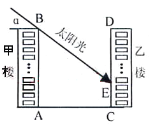
【题目】下图为某小区的两幢1O层住宅楼,由地面向上依次为第1层、第2层、…、第10层,每层的高度为3m,两楼间的距离AC=30m.现需了解在某一时段内,甲楼对乙楼的采光的影响情况.假设某一时刻甲楼楼顶B落在乙楼的影子长EC=h,太阳光线与水平线的夹角为α.
(1)用含α的式子表示h;
(2)当α=30°时,甲楼楼顶B的影子落在乙楼的第几层?从此时算起,若α每小时增加10°,几小时后,甲楼的影子刚好不影响乙楼采光.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则下列结论:①4ac﹣b2<0;②2a﹣b=0;③a+b+c<0;④点M(x1,y1)、N(x2,y2)在抛物线上,若x1<x2<﹣1,则y1>y2,⑤abc>0.其中正确结论的个数是( )

A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
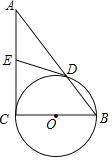
【题目】如图,在△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,⊙O的切线DE交AC于点E.
(1)求证:E是AC中点;
(2)若AB=10,BC=6,连接CD,OE,交点为F,求OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,AB是⊙O的直径,⊙O交BC于点D,DE⊥AC于点E,BE交⊙O于点F,连接AF,AF的延长线交DE于点P.
(1)求证:DE是⊙O的切线;
(2)求tan∠ABE的值;
(3)若OA=2,求线段AP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(14分)如图,已知抛物线![]() (
(![]() )与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C,且OC=OB.
)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C,且OC=OB.

(1)求此抛物线的解析式;
(2)若点E为第二象限抛物线上一动点,连接BE,CE,求四边形BOCE面积的最大值,并求出此时点E的坐标;
(3)点P在抛物线的对称轴上,若线段PA绕点P逆时针旋转90°后,点A的对应点A′恰好也落在此抛物线上,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
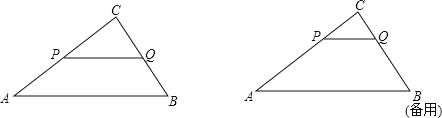
【题目】如图:已知△ABC中,AB=5,BC=3,AC=4,PQ∥AB,P点在AC上(与A、C不重合),Q在BC上.
(1)当△PQC的面积与四边形PABQ的面积相等时,求CP的长;
(2)当△PQC的周长与四边形PABQ的周长相等时,求CP的长;
(3)试问:在AB上是否存在一点M,使得△PQM为等腰直角三角形?若不存在,请简要说明理由;若存在,请求出PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=![]() ,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE,CF.
,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE,CF.

(1)若A,E,O三点共线,求CF的长;
(2)求△CDF的面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com