
【题目】如图,点C是线段AB的中点,延长线段AB至点D,使BD=AB,延长AD至点E,使DE=AC.
![]()
(1)依题意画出图形(尺规作图),则![]() =_________(直接写出结果);
=_________(直接写出结果);
(2)若DE=3,求AB的长;
(3)请写出与BE长度相同的线段.
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】为顺利通过“文明城市”验收,盐城市政府拟对部分地区进行改造,根据市政建设需要,须在16天之内完成工程.现有甲、乙两个工程队,经调查知道:乙队单独完成此工程的时间是甲队单独完成此工程时间的2倍,若甲、乙两队合作只需12天完成.
(1)求甲、乙工程队单独完成这项工程各需要多少天?
(2)两队合作完成此项工程,若甲队参与施工a天,乙队参与施工b天,试用含a的代数式表示b;
(3)若甲队每天的工程费用是0.6万元, 乙队每天的工程费用是0.25万元,请你设计一种方案,既能按时完工,又能使工程费最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知2a﹣1的平方根是±3,3a+b﹣9的立方根是2,c是![]() 的整数部分,求a+2b+c的值.
的整数部分,求a+2b+c的值.
(2)有四个实数分别为32,![]() ,
,![]() ,
,![]() .
.
①请你计算其中有理数的和.
②若x﹣2是①中的和的平方,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)如图,已知抛物线![]() 经过
经过![]() ,
,![]() 两点,顶点为
两点,顶点为![]() .
.
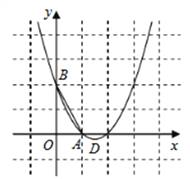
(1)求抛物线的解析式;
(2)将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 后,点
后,点![]() 落在点
落在点![]() 的位置,将抛物线沿
的位置,将抛物线沿![]() 轴平移后经过点
轴平移后经过点![]() ,求平移后所得图象的函数关系式;
,求平移后所得图象的函数关系式;
(3)设(2)中平移后,所得抛物线与![]() 轴的交点为
轴的交点为![]() ,顶点为
,顶点为![]() ,若点
,若点![]() 在平移后的抛物线上,且满足
在平移后的抛物线上,且满足![]() 的面积是
的面积是![]() 面积的2倍,求点
面积的2倍,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AM∥BN,∠A=60°,点P是射线AM上一动点(不与点A重合).BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
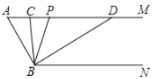
(发现)
(1)∵AM∥BN,∴∠ACB=_______;(填相等的角)
(2)求∠ABN、∠CBD的度数;
解:∵AM∥BN,
∴∠ABN+∠A=180°,
∵∠A=60°,
∴∠ABN=∠ABP+∠PBN=______,
∵BC平分∠ABP,BD平分∠PBN,
∴∠ABP=2∠CBP,∠PBN=______,
∴2∠CBP+2∠DBP=120°,
∴∠CBD=∠CBP+∠DBP=______.
(操作)
(3)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),在某年某月的日历中,任意圈出一竖列相邻的三个数,设中间的一个数为![]() ,则用含
,则用含![]() 的代数式表示这三个数分别是__________;(按从小到大的顺序写在横线上)
的代数式表示这三个数分别是__________;(按从小到大的顺序写在横线上)
(2)现将连续自然数1~2007按图(2)的方式排成一个长方形阵形然后用一个正方形框出16个数.
①图中框出的这16个数的和是__________;
②在图(2)中,要使一个正方形框出的16个数的和等于2016,2168,是否可能?若不可能,请说明理由;若有可能,请求出该正方形框出的16个数中的最小数和最大数.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.
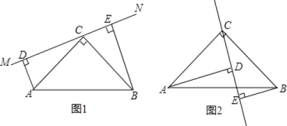
(1)求证:①△ADC≌△CEB;②DE=AD+BE.
(2)当直线MN绕点C旋转到图2的位置时,DE、AD、BE又怎样的关系?并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线过点A(2,0),B(-1,0),与y轴交于点C,且OC=2.则这条抛物线的表达式为( )
A. y=x2-x-2
B. y=-x2+x+2
C. y=x2-x-2或y=-x2+x+2
D. y=-x2-x-2或y=x2+x+2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com