
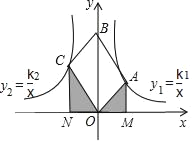
【题目】如图,四边形OABC是平行四边形,对角线OB在y轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y1=![]() 和y2=
和y2=![]() 的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:①
的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:①![]() ②阴影部分面积是
②阴影部分面积是![]() (k1﹣k2)③当∠AOC=90°时,|k1|=|k2|;④若四边形OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是_____.
(k1﹣k2)③当∠AOC=90°时,|k1|=|k2|;④若四边形OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是_____.
【答案】①②④.
【解析】
作AE⊥y轴于点E,CF⊥y轴于点F,根据平行四边形的性质得S△AOB=S△COB,利用三角形面积公式得到AE=CF,则有OM=ON,再利用反比例函数k的几何意义和三角形面积公式得到S△AOM=![]() |k1|=
|k1|=![]() OMAM,S△CON=
OMAM,S△CON=![]() |k2|=ONCN,所以有
|k2|=ONCN,所以有![]() ;由S△AOM=
;由S△AOM=![]() |k1|,S△CON=
|k1|,S△CON=![]() |k2|,得到S阴影=S△AOM+S△CON=
|k2|,得到S阴影=S△AOM+S△CON=![]() (|k1|+|k2|)=
(|k1|+|k2|)=![]() (k1-k2);当∠AOC=90°,得到四边形OABC是矩形,由于不能确定OA与OC相等,则不能判断△AOM≌△CNO,所以不能判断AM=CN,则不能确定|k1|=|k2|;若OABC是菱形,根据菱形的性质得OA=OC,可判断Rt△AOM≌Rt△CNO,则AM=CN,所以|k1|=|k2|,即k1=-k2,根据反比例函数的性质得两双曲线既关于x轴对称,也关于y轴对称.
(k1-k2);当∠AOC=90°,得到四边形OABC是矩形,由于不能确定OA与OC相等,则不能判断△AOM≌△CNO,所以不能判断AM=CN,则不能确定|k1|=|k2|;若OABC是菱形,根据菱形的性质得OA=OC,可判断Rt△AOM≌Rt△CNO,则AM=CN,所以|k1|=|k2|,即k1=-k2,根据反比例函数的性质得两双曲线既关于x轴对称,也关于y轴对称.
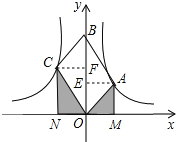
作AE⊥y轴于E,CF⊥y轴于F,如图,
∵四边形OABC是平行四边形,
∴S△AOB=S△COB,
∴AE=CF,
∴OM=ON,
∵S△AOM=![]() |k1|=
|k1|=![]() OMAM,S△CON=
OMAM,S△CON=![]() |k2|=
|k2|=![]() ONCN,
ONCN,
∴![]() ,故①正确;
,故①正确;
∵S△AOM=![]() |k1|,S△CON=
|k1|,S△CON=![]() |k2|,
|k2|,
∴S阴影部分=S△AOM+S△CON=![]() (|k1|+|k2|),
(|k1|+|k2|),
而k1>0,k2<0,
∴S阴影部分=![]() (k1-k2),故②正确;
(k1-k2),故②正确;
当∠AOC=90°,
∴四边形OABC是矩形,
∴不能确定OA与OC相等,
而OM=ON,
∴不能判断△AOM≌△CNO,
∴不能判断AM=CN,
∴不能确定|k1|=|k2|,故③错误;
若OABC是菱形,则OA=OC,
而OM=ON,
∴Rt△AOM≌Rt△CNO,
∴AM=CN,
∴|k1|=|k2|,
∴k1=-k2,
∴两双曲线既关于x轴对称,也关于y轴对称,故④正确,
故答案为:①②④.


科目:初中数学 来源: 题型:
【题目】甲、乙两大型超市为了吸引顾客,都举行有奖酬宾活动,凡购物满200元,均可得到一次抽奖的机会,在一个纸盒里装有2个红球和2个白球,除颜色外其它都相同,抽奖者一次从中摸出两个球,根据球的颜色决定送礼金券(在他们超市使用时,与人民币等值)的多少(如下表).
甲超市.
球 | 两 红 | 一红一白 | 两 白 |
礼金券(元) | 20 | 50 | 20 |
乙超市:
球 | 两 红 | 一红一白 | 两 白 |
礼金券(元) | 50 | 20 | 50 |
【1】(1)用树状图表示得到一次摸奖机会时中礼金券的所有情况;
【2】(2)如果只考虑中奖因素,你将会选择去哪个超市购物?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】原来公园有一个半径为 1 m 的苗圃,现在准备扩大面积,设当扩大后的半径为x m时,则增加的环形的面积为y m 2 .
(1)写出y与x的函数关系式;
(2)当半径增大到多少时面积增大1倍;
(3)试猜测半径是多少时,面积是原来的3、4、5、…倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,sinA=![]() ,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
(1)求线段CD的长;
(2)求cos∠ABE的值。

查看答案和解析>>
科目:初中数学 来源: 题型:
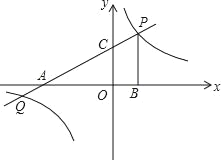
【题目】如图,直线y=![]() x+b分别交x轴、y轴于点A、C,点P是直线AC与双曲线y=
x+b分别交x轴、y轴于点A、C,点P是直线AC与双曲线y=![]() 在第一象限内的交点,PB⊥x轴,垂足为点B,且OB=2,PB=4.
在第一象限内的交点,PB⊥x轴,垂足为点B,且OB=2,PB=4.
(1)求反比例函数的解析式;
(2)求△APB的面积;
(3)求在第一象限内,当x取何值时一次函数的值小于反比例函数的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】砀山酥梨是一种驰名中外的特色水果,它是梨的一种,因为出产于砀山县而得名。现有20筐砀山酥梨,以每筐25千克的质量为标准,超过或不足的千克数分别用正、负数来表示,记录如下:

(1)这20筐砀山酥梨中,最重的一筐比最轻的一筐重多少千克?
(2)与标准质量比较,这20筐砀山酥梨总计超过或不足多少千克?
(3)若砀山酥梨每千克售价4元,则这20筐砀山酥梨可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,已知抛物线y=ax2+bx﹣5与x轴交于A(﹣1,0),B(5,0)两点,与y轴交于点C.
(1)求抛物线的函数表达式;
(2)如图2,CE∥x轴与抛物线相交于点E,点H是直线CE下方抛物线上的动点,过点H且与y轴平行的直线与BC,CE分别相交于点F,G,试探究当点H运动到何处时,四边形CHEF的面积最大,求点H的坐标;
(3)若点K为抛物线的顶点,点M(4,m)是该抛物线上的一点,在x轴,y轴上分别找点P,Q,使四边形PQKM的周长最小,求出点P,Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.
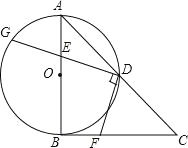
(1)求证:AE=BF;
(2)连接GB,EF,求证:GB∥EF;
(3)若AE=1,EB=2,求DG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com