
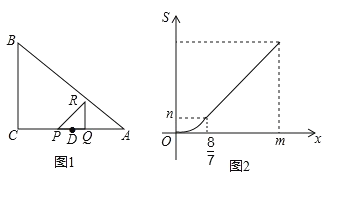
【题目】如图1,在△ABC中,∠C=90°,点D在AC上,且CD>DA,DA=2.点P、Q同时从D点出发,以相同的速度分别沿射线DC、射线DA运动.过点Q作AC的垂线段QR,使QR=PQ,联接PR.当点Q到达A时,点P、Q同时停止运动.设PQ=x.△PQR和△ABC重合部分的面积为S.S关于x的函数图像如图2所示(其中0<x≤![]() ,
,![]() <x≤m时,函数的解析式不同)
<x≤m时,函数的解析式不同)
(1)填空:n的值为___________;
(2)求S关于x的函数关系式,并写出x的取值范围.
科目:初中数学 来源: 题型:
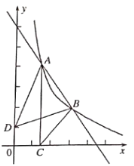
【题目】如图,点![]() 、
、![]() 是直线
是直线![]() 与反比例函数
与反比例函数![]() 图象的两个交点,
图象的两个交点,![]() 轴于点C,己知点D(0,1),连接AD、BD、BC,
轴于点C,己知点D(0,1),连接AD、BD、BC,
(1)求反比例函数和直线AB的表达式;
(2)根据函数图象直接写出当![]() 时不等式
时不等式![]() 的解集;
的解集;
(3)设△ABC和△ABD的面积分别为![]() 、
、![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,连接AC,将![]() 绕点A逆时针旋转α得
绕点A逆时针旋转α得![]() ,连接CF,O为CF的中点,连接OE,OD.
,连接CF,O为CF的中点,连接OE,OD.
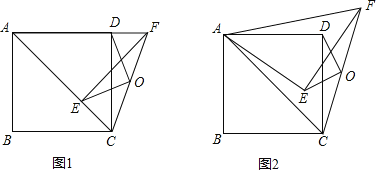
(1)如图1,当![]() 时,请直接写出OE与OD的关系(不用证明).
时,请直接写出OE与OD的关系(不用证明).
(2)如图2,当![]() 时,(1)中的结论是否成立?请说明理由.
时,(1)中的结论是否成立?请说明理由.
(3)当![]() 时,若
时,若![]() ,请直接写出点O经过的路径长.
,请直接写出点O经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某医药研究所研发了一种新药,试验药效时发现:1.5小时内,血液中含药量y(微克)与时间x(小时)的关系可近似地用二次函数y=ax2+bx表示;1.5小时后(包括1.5小时),y与x可近似地用反比例函数y=![]() (k>0)表示,部分实验数据如表:
(k>0)表示,部分实验数据如表:
时间x(小时) | 0.2 | 1 | 1.8 | … |
含药量y(微克) | 7.2 | 20 | 12.5 | … |
(1)求a、b及k的值;
(2)服药后几小时血液中的含药量达到最大值?最大值为多少?
(3)如果每毫升血液中含药量不少于10微克时治疗疾病有效,那么成人按规定剂量服用该药一次后能维持多长的有效时间.(![]() ≈1.41,精确到0.1小时)
≈1.41,精确到0.1小时)
查看答案和解析>>
科目:初中数学 来源: 题型:
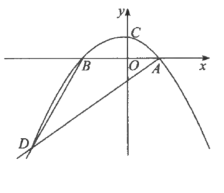
【题目】如图,在平面直角坐标系中,抛物线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,且经过点
,且经过点![]() ,连接
,连接![]() .
.
(1)求该抛物线的函数关系式;
(2)△ANM与![]() 是否相似?若相似,请求出此时点
是否相似?若相似,请求出此时点![]() 、点
、点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)若点![]() 是直线
是直线![]() 上方的抛物线上一动点(不与点
上方的抛物线上一动点(不与点![]() 重合),过
重合),过![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,以
,以![]() 为直径作⊙
为直径作⊙![]() ,则⊙
,则⊙![]() 在直线
在直线![]() 上所截得的线段长度的最大值等于 .(直接写出答案)
上所截得的线段长度的最大值等于 .(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=x2+(k﹣1)x﹣k与直线y=kx+1交于A,B两点,点A在点B的左侧.


(1)如图1,当k=1时,直接写出A,B两点的坐标;
(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;
(3)如图2,抛物线y=x2+(k﹣1)x﹣k(k>0)与x轴交于点C、D两点(点C在点D的左侧),在直线y=kx+1上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学具专卖店试销一种成本为60元/套的学具.规定试销期间销售单价不得低于成本单价,且获利不得高于成本价的20%,该专卖店每天的固定费用是100元.试销发现,每件销售单价相对成本提高x元(x为整数)与日平均销售量y件之间符合一次函数关系,且当x=10时,y=40;x=25时,y=10.
(1)求y与x之间的关系式;
(2)该学具专卖店日平均获得毛利润为w元(毛利润=利润﹣固定费用),求当销售单价为多少元时,日平均毛利润最大,最大日平均毛利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
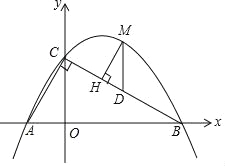
【题目】如图,直线y=﹣![]() x+
x+![]() 分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+
分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+![]() 经过A,B两点.
经过A,B两点.
(1)求A、B两点的坐标;
(2)求抛物线的解析式;
(3)点M是直线BC上方抛物线上的一点,过点M作MH⊥BC于点H,作MD∥y轴交BC于点D,求△DMH周长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情防控,我们一直在坚守.某居委会组织两个检查组,分别对“居民体温”和“居民安全出行”的情况进行抽查.若这两个检查组在辖区内的某三个校区中各自随机抽取一个小区进行检查,则他们恰好抽到同一个小区的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com