
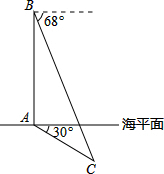
 在中俄“海上联合-2014”反潜演习中,我军舰A测得潜艇C的俯角为30°,位于军舰A正上方325米的反潜直升机B测得潜艇C的俯角为68°,试根据以上数据求出潜艇C离开海平面的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5,$\sqrt{3}$≈1.7)
在中俄“海上联合-2014”反潜演习中,我军舰A测得潜艇C的俯角为30°,位于军舰A正上方325米的反潜直升机B测得潜艇C的俯角为68°,试根据以上数据求出潜艇C离开海平面的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5,$\sqrt{3}$≈1.7) 分析 过点C作CD⊥AB,交BA的延长线于点D,则AD就是潜艇C的下潜深度.设AD=x,则BD=BA+AD=325+x,在Rt△ACD中,列出325+x=$\sqrt{3}$x•tan68°即可解答.
解答 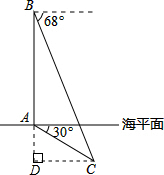 解:如图,过点C作CD⊥AB,交BA的延长线于点D,则AD就是潜艇C的下潜深度.
解:如图,过点C作CD⊥AB,交BA的延长线于点D,则AD就是潜艇C的下潜深度.
由题意,得∠ACD=30°,∠BCD=68°.设AD=x,则BD=BA+AD=325+x,
在Rt△ACD中,CD=$\frac{AD}{tan∠ACD}$=$\frac{x}{tan30°}$=$\sqrt{3}$x,
在Rt△BCD中,BD=CD•tan68°,
则325+x=$\sqrt{3}$x•tan68°.
解得:x=$\frac{325}{\sqrt{3}tan68°-1}$≈$\frac{325}{1.7×2.5-1}$=100.
答:潜艇C的下潜深度约为100米.
点评 本题考查了解直角三角形的应用--仰角俯角问题,要求学生能借助仰角、俯角构造直角三角形并解直角三角形.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 96人 | B. | 90人 | C. | 64人 | D. | 50人 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,菱形ABCD在平面直角坐标系中,点A位坐标原点,点B在x轴正半轴上,若点D的坐标为(1,$\sqrt{3}$),则点C的坐标为(3,$\sqrt{3}$).
如图,菱形ABCD在平面直角坐标系中,点A位坐标原点,点B在x轴正半轴上,若点D的坐标为(1,$\sqrt{3}$),则点C的坐标为(3,$\sqrt{3}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com