
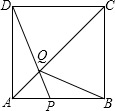
 ČēĶ¼£¬ŌŚ±ß³¤ĪŖ4µÄÕż·½ŠĪABCDÖŠ£¬µćPŌŚABÉĻ“ÓAĻņBŌĖ¶Æ£¬Į¬½įDP½»ACÓŚµćQ£®
ČēĶ¼£¬ŌŚ±ß³¤ĪŖ4µÄÕż·½ŠĪABCDÖŠ£¬µćPŌŚABÉĻ“ÓAĻņBŌĖ¶Æ£¬Į¬½įDP½»ACÓŚµćQ£®·ÖĪö £Ø1£©øł¾ŻÕż·½ŠĪŠŌÖŹµĆ³öAB=AD£¬”ĻBAD=90”ć£¬”ĻDAC=”ĻBAC=45”ć£¬ĄūÓĆ”°±ß½Ē±ß”±Ö¤Ć÷”÷ADQ”Õ”÷ABQ¼“æÉ£»
£Ø2£©¹żµćQ×÷QE”ĶADÓŚE£¬ĄūÓĆ”÷ABQµÄĆ껿ŹĒÕż·½ŠĪABCDĆ껿µÄ$\frac{1}{6}$Ēó³öQE£¬½ų¶ųĒó³öDE×īŗóÓĆ¹“¹É¶ØĄķ¼“æÉ£»
£Ø3£©µćPŌĖ¶ÆŹ±£¬”÷ADQĒ”ĪŖµČŃüČż½ĒŠĪµÄĒéæöÓŠČżÖÖ£ŗQD=QA»ņDA=DQ»ņAQ=AD£®
¢Łµ±µćPŌĖ¶Æµ½ÓėµćBÖŲŗĻŹ±£¬QD=QA£¬“ĖŹ±”÷ADQŹĒµČŃüČż½ĒŠĪ£»
¢Śµ±µćPÓėµćCÖŲŗĻŹ±£¬µćQÓėµćCŅ²ÖŲŗĻ£¬“ĖŹ±DA=DQ£¬”÷ADQŹĒµČŃüČż½ĒŠĪ£»
¢Ūµ±AD=AQ=4Ź±£¬ÓŠCP=CQ£¬CP=AC-AD¶ųÓÉÕż·½ŠĪµÄ¶Ō½ĒĻߵĊŌÖŹµĆµ½CPµÄÖµ£®
½ā“š £Ø1£©Ö¤Ć÷£ŗ”ßĖıߊĪABCDŹĒÕż·½ŠĪ
”ąAD=AB£¬”ĻDAQ=”ĻBAQ=45”ć
ÓÖ AQ=AQ£¬
”ą”÷ADQ”Õ”÷ABQ
¼“ ĪŽĀŪµćPŌĖ¶Æµ½ABÉĻŗĪ“¦Ź±£¬¶¼ÓŠ”÷ADQ”Õ”÷ABQ
£Ø2£©ČēĶ¼1£¬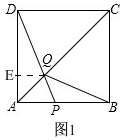
×÷ QE”ĶADÓŚE£¬ÓÉ£Ø1£©µĆ”÷ADQ”Õ”÷ABQ£¬
”ąS”÷ADQ=S”÷ABQ
”ß”÷ABQµÄĆ껿ŹĒÕż·½ŠĪABCDĆ껿µÄ$\frac{1}{6}$
”ą$\frac{1}{2}$AD”ĮQE=$\frac{1}{6}$SÕż·½ŠĪABCD=$\frac{8}{3}$£¬
”ąQE=$\frac{4}{3}$
ÓÖ”ßQE”ĶAD£¬”ĻDAQ=45”ć
”ą”ĻAQE=”ĻDAQ=45”ć
”ąAE=QE=$\frac{4}{3}$
”ąDE=4-$\frac{4}{3}$=$\frac{8}{3}$
”ąŌŚRt”÷DEQÖŠ£¬QE=$\frac{4}{3}$£¬DE=$\frac{8}{3}$£¬
øł¾Ż¹“¹É¶ØĄķµĆ£¬DQ=$\frac{4\sqrt{5}}{3}$
£Ø3£©Čō”÷ADQŹĒµČŃüČż½ĒŠĪ£¬ŌņÓŠQD=QA»ņDA=DQ»ņAQ=AD£¬
¢Łµ±µćPŌĖ¶Æµ½ÓėµćBÖŲŗĻŹ±£¬ÓÉÕż·½ŠĪÖŖQD=QA“ĖŹ±”÷ADQŹĒµČŃüČż½ĒŠĪ£»
¢Śµ±µćPÓėµćCÖŲŗĻŹ±£¬µćQÓėµćCÖŲŗĻ£¬“ĖŹ±DA=DQ£¬”÷ADQŹĒµČŃüČż½ĒŠĪ£»
¢ŪČēĶ¼4£¬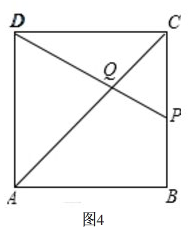 ÉčµćPŌŚBC±ßÉĻŌĖ¶Æµ½CP=xŹ±£¬ÓŠAD=AQ£¬
ÉčµćPŌŚBC±ßÉĻŌĖ¶Æµ½CP=xŹ±£¬ÓŠAD=AQ£¬
”ßAD”ĪBC
”ą”ĻADQ=”ĻCPQ£®
Ó֔ߔĻAQD=”ĻCQP£¬”ĻADQ=”ĻAQD£¬
”ą”ĻCQP=”ĻCPQ£®
”ąCQ=CP=x£®
”ßAC=4$\sqrt{2}$£¬AQ=AD=4£®
”ąx=CQ=AC-AQ=4$\sqrt{2}$-4£®
¼“µ±CP=4$\sqrt{2}$-4Ź±£¬”÷ADQŹĒµČŃüČż½ĒŠĪ£®
µćĘĄ ±¾ĢāŹĒĖıߊĪ×ŪŗĻĢā£¬Ö÷ŅŖæ¼²éĮĖÕż·½ŠĪµÄŠŌÖŹ”¢Č«µČČż½ĒŠĪµÄÅŠ¶ØÓėŠŌÖŹ”¢Čż½ĒŠĪµÄĆ껿¹«Ź½”¢µČŃüČż½ĒŠĪµÄŠŌÖŹ”¢µČŃüÖ±½ĒČż½ĒŠĪµÄŠŌÖŹµČÖŖŹ¶£»±¾Ģā×ŪŗĻŠŌĒ棬ÄŃ¶Č½Ļ“󣬣Ø3£©ŠčŅŖ·ÖĄąĢÖĀŪ£®


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 ČēĶ¼£¬
ČēĶ¼£¬²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
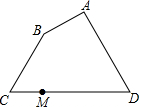
 ŌŚRt”÷ABCÖŠ£¬”ĻACB=90”ć£¬AC=8£¬BC=6£¬µćDŹĒŅŌµćAĪŖŌ²ŠÄ4ĪŖ°ė¾¶µÄŌ²ÉĻŅ»µć£¬Į¬½ÓBD£¬µćMĪŖBDÖŠµć£¬Ļ߶ĪCM³¤¶ČµÄ×ī“óÖµĪŖ7£®
ŌŚRt”÷ABCÖŠ£¬”ĻACB=90”ć£¬AC=8£¬BC=6£¬µćDŹĒŅŌµćAĪŖŌ²ŠÄ4ĪŖ°ė¾¶µÄŌ²ÉĻŅ»µć£¬Į¬½ÓBD£¬µćMĪŖBDÖŠµć£¬Ļ߶ĪCM³¤¶ČµÄ×ī“óÖµĪŖ7£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
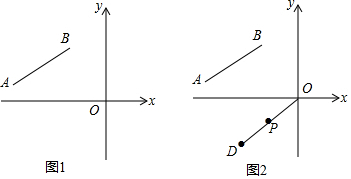
 ČēĶ¼£¬Ę½ŠŠĖıߊĪABCDÖŠ£¬µćE”¢F·Ö±šŌŚAD”¢ABÉĻ£¬ŅĄ“ĪĮ¬½ÓEB”¢EC”¢FC”¢FD£¬Ķ¼ÖŠŅõÓ°²æ·ÖµÄĆ껿·Ö±šĪŖS1”¢S2”¢S3”¢S4£¬ŅŃÖŖS1=2”¢S2=12”¢S3=3£¬ŌņS4µÄÖµŹĒ7£®
ČēĶ¼£¬Ę½ŠŠĖıߊĪABCDÖŠ£¬µćE”¢F·Ö±šŌŚAD”¢ABÉĻ£¬ŅĄ“ĪĮ¬½ÓEB”¢EC”¢FC”¢FD£¬Ķ¼ÖŠŅõÓ°²æ·ÖµÄĆ껿·Ö±šĪŖS1”¢S2”¢S3”¢S4£¬ŅŃÖŖS1=2”¢S2=12”¢S3=3£¬ŌņS4µÄÖµŹĒ7£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā

| A£® | 9cm2 | B£® | 18cm2 | C£® | 27cm2 | D£® | 72cm2 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
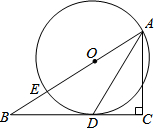 ČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻC=90”ć£¬µćEŌŚABÉĻ£¬ŅŌAEĪŖÖ±¾¶µÄ”ŃOÓėBCĻąĒŠÓŚµćD£¬Į¬½ÓAD£®
ČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻC=90”ć£¬µćEŌŚABÉĻ£¬ŅŌAEĪŖÖ±¾¶µÄ”ŃOÓėBCĻąĒŠÓŚµćD£¬Į¬½ÓAD£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
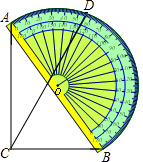 ČēĶ¼£¬Ņ»æéÖ±½ĒČż½Ē°åABCµÄŠ±±ßABÓėĮæ½ĒĘ÷µÄÖ±¾¶ÖŲŗĻ£¬µćD¶ŌÓ¦54”ć£¬Ōņ”ĻBCDµÄ¶ČŹżĪŖ£Ø””””£©
ČēĶ¼£¬Ņ»æéÖ±½ĒČż½Ē°åABCµÄŠ±±ßABÓėĮæ½ĒĘ÷µÄÖ±¾¶ÖŲŗĻ£¬µćD¶ŌÓ¦54”ć£¬Ōņ”ĻBCDµÄ¶ČŹżĪŖ£Ø””””£©| A£® | 63”ć | B£® | 54”ć | C£® | 36”ć | D£® | 27”ć |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com