
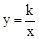 (x>0)交于D点,过点D作DC⊥x轴,垂足为G,连接OD.已知△AOB≌△ACD.
(x>0)交于D点,过点D作DC⊥x轴,垂足为G,连接OD.已知△AOB≌△ACD.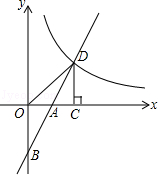
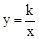 ( x>0)的图象上,∴k=2×2=4。
( x>0)的图象上,∴k=2×2=4。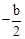 ,0),B(0,b),
,0),B(0,b),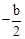 ,
,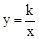 ( x>0)的图象上,
( x>0)的图象上,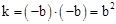 ,即k与b的数量关系为:
,即k与b的数量关系为: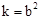 。
。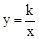 ( x>0)的图象上求出k的值。
( x>0)的图象上求出k的值。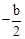 ,0),B(0,b),再根据△AOB≌△ACD得到CD=DB,AO=AC,即可求出D坐标,把D点坐标代入反比例函数解析式求出k和b之间的关系,进而也可以求出直线OD的解析式。
,0),B(0,b),再根据△AOB≌△ACD得到CD=DB,AO=AC,即可求出D坐标,把D点坐标代入反比例函数解析式求出k和b之间的关系,进而也可以求出直线OD的解析式。

科目:初中数学 来源:不详 题型:解答题
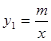 的图象与一次函数
的图象与一次函数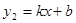 的图象交于点M,N,已点M的坐标为(1,3),点N的纵坐标为-1.
的图象交于点M,N,已点M的坐标为(1,3),点N的纵坐标为-1.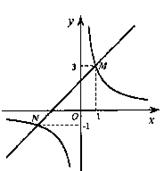
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
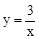 (x>0)的图象上,AB垂直于x轴,垂足为点B,将△ABO沿x轴向右平移2个单位长度,得到Rt△DEF,点D落在反比例函数
(x>0)的图象上,AB垂直于x轴,垂足为点B,将△ABO沿x轴向右平移2个单位长度,得到Rt△DEF,点D落在反比例函数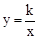 (x>0)的图象上.
(x>0)的图象上.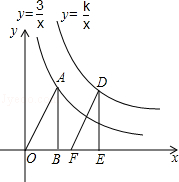
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
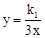 的图象与一次函数
的图象与一次函数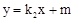 的图象交于A
的图象交于A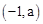 、B
、B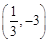 两点,连结AO。
两点,连结AO。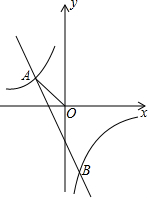
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (x>
(x> )图象上一点P,PA⊥x轴于点A(a,0),点B坐标为(0,b)(b>0),动点M是y轴正半轴上B点上方的点,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q,连结AQ,取AQ的中点为C.
)图象上一点P,PA⊥x轴于点A(a,0),点B坐标为(0,b)(b>0),动点M是y轴正半轴上B点上方的点,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q,连结AQ,取AQ的中点为C.
 ,求此时P点的坐标;
,求此时P点的坐标;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com