
【题目】已知实数a , b满足a-b=1,a2-ab+2>0,当1≤x≤2时,函数y= ![]() (a≠0)的最大值与最小值之差是1,求a的值
(a≠0)的最大值与最小值之差是1,求a的值
【答案】解答:∵a2-ab+2>0,
∴a2-ab>-2,
a(a-b)>-2,
∵a-b=1,
∴a>-2,
① -2<a<0,1≤x≤2时,函数y= ![]() 的最大值是y=
的最大值是y= ![]() ,最小值是y=a ,
,最小值是y=a ,
∵最大值与最小值之差是1,
∴ ![]() -a=1,
-a=1,
解得:a=-2,不合题意,舍去;
②当a>0,1≤x≤2时,函数y= ![]() 的最大值是y=a , 最小值是y=
的最大值是y=a , 最小值是y= ![]() ∵最大值与最小值之差是1,
∵最大值与最小值之差是1,
∴a- ![]() =1,
=1,
解得:a=2,符合题意,
∴a的值是2.
【解析】首先根据条件a-b=1,a2-ab+2>0可确定a>-2,然后再分情况进行讨论:①当-2<a<0,1≤x≤2时,函数y= ![]() 的最大值是y=
的最大值是y= ![]() ,最小值是y=a , ②当a>0,1≤x≤2时,函数y=
,最小值是y=a , ②当a>0,1≤x≤2时,函数y= ![]() 的最大值是y=a , 最小值是y=
的最大值是y=a , 最小值是y= ![]() ,再分别根据最大值与最小值之差是1,计算出a的值
,再分别根据最大值与最小值之差是1,计算出a的值
【考点精析】根据题目的已知条件,利用反比例函数的图象和反比例函数的性质的相关知识可以得到问题的答案,需要掌握反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点;性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.


科目:初中数学 来源: 题型:
【题目】(本小题满分8分)某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体实验.测得成人服药后血液中药物深度![]() (微克/毫升)与服药时间
(微克/毫升)与服药时间![]() 小时之间的函数关系如图所示(当
小时之间的函数关系如图所示(当![]() 时,
时,![]() 与
与![]() 成反比).
成反比).

(1)根据图象分别求出血液中药物浓度上升和下降阶段![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)问血液中药物浓度不低于4微克/毫升的持续时间为多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于函数y= ![]() ,下列说法错误的是( )。
,下列说法错误的是( )。
A.这个函数的图象位于第一、第三象限
B.这个函数的图象既是轴对称图形又是中心对称图形
C.当x>0时,y随x的增大而增大
D.当x<0时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y= ![]() 的图象的一支位于第一象限.
的图象的一支位于第一象限.
(1)判断该函数图象的另一支所在的象限,并求m的取值范围;
(2)如图,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于x轴对称,若△OAB的面积为6,求m的值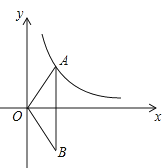
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰△ABC中,AB=AC,则有BC边上的中线,高线和∠BAC的平分线重合于AD(如图一).若将等腰△ABC的顶点A向右平行移动后,得到△A′BC(如图二),那么,此时BC边上的中线、BC边上的高线和∠BA′C的平分线应依次分别是 , , .(填A′D、A′E、A′F)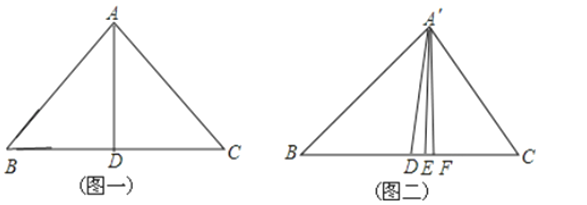
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学进行了6轮投篮比赛,两人的得分情况统计如下:

下列说法不正确的是( )
A. 甲得分的极差小于乙得分的极差 B. 甲得分的中位数大于乙得分的中位数
C. 甲得分的平均数大于乙得分的平均数 D. 乙的成绩比甲的成绩稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车厂改进生产工艺后,每天生产的汽车比原来每天生产的汽车多6辆,那么现在15天的产量就超过了原来20天的产量,设原来每天生产汽车x辆,则列出的不等式为( )
A. 15x>20(x+6) B. 15(x+6)>20x C. 15x>20(x-6) D. 15(x-6)>20x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c经过A(﹣3,0),B(1,0),C(0,3)三点,其顶点为D,对称轴是直线l,l与x轴交于点H.
(1)求该抛物线的解析式;
(2)若点P是该抛物线对称轴l上的一个动点,求△PBC周长的最小值;
(3)如图(2),若E是线段AD上的一个动点( E与A、D不重合),过E点作平行于y轴的直线交抛物线于点F,交x轴于点G,设点E的横坐标为m,△ADF的面积为S.
①求S与m的函数关系式;
②S是否存在最大值?若存在,求出最大值及此时点E的坐标; 若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com