
【题目】如图,在Rt△ABC中,点D在直角边BC上,DE平分∠ADB,∠1=∠2=∠3,AC=5cm.
(1)求∠3的度数;
(2)判断DE与AB的位置关系,并说明理由;
(3)求BE的长.

【答案】(1)∠3=30°;(2)DE⊥AB;(3)BE=5cm.
【解析】
(1)根据三角形内角和定理解答;
(2)根据已知条件∠2=∠3、DE平分∠ADB,可以判定DE是等腰△ABD底边AB上的中垂线,即DE⊥AB;
(3)利用(1)中的30°的∠3所对的直角边是斜边的一半知AC=![]() AB;然后根据(2)中的DE是边AB的中垂线的性质知BE=
AB;然后根据(2)中的DE是边AB的中垂线的性质知BE=![]() AB;所以BE=AC=5cm.
AB;所以BE=AC=5cm.
解:(1)在Rt△ABC中,∠C=90°,∠1=∠2=∠3,
∴∠1+∠2+∠3=90°,即3∠3=90°,
∴∠3=30°;
(2)DE⊥AB.
理由:在△ADB中,∠2=∠3,
∴△ADB是等腰三角形;
又∵DE平分∠ADB,
∴DE是边AB上的中垂线,
∴DE⊥AB;
(3)由(1)知,Rt△ABC中,∠3=30°,
∴AC=![]() AB(30°角所对的直角边是斜边的一半);
AB(30°角所对的直角边是斜边的一半);
又由(2)知,DE是边AB上的中垂线,
∴BE=![]() AB,
AB,
∴BE=AC=5cm.


科目:初中数学 来源: 题型:
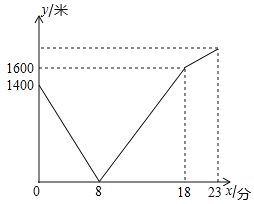
【题目】小婷家与学校之间是一条笔直的公路,小婷从家步行前往学校的途中发现忘记带昨天的回家作业本,便向路人借了手机打给妈妈,妈妈接到电话后,带上作业本马上赶往学校,同时小婷沿原路返回![]() 两人相遇后,小婷立即赶往学校,妈妈沿原路返回家,并且小婷到达学校比妈妈到家多用了5分钟,若小婷步行的速度始终是每分钟100米,小婷和妈妈之间的距离y与小婷打完电话后步行的时间x之间的函数关系如图所示
两人相遇后,小婷立即赶往学校,妈妈沿原路返回家,并且小婷到达学校比妈妈到家多用了5分钟,若小婷步行的速度始终是每分钟100米,小婷和妈妈之间的距离y与小婷打完电话后步行的时间x之间的函数关系如图所示
![]() 妈妈从家出发______分钟后与小婷相遇;
妈妈从家出发______分钟后与小婷相遇;
![]() 相遇后妈妈回家的平均速度是每分钟______米,小婷家离学校的距离为______米
相遇后妈妈回家的平均速度是每分钟______米,小婷家离学校的距离为______米![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,下列说法①a>0;②b2﹣4ac>0;③4a+2b+c>0;④c<0;⑤b>0.其中正确的有( )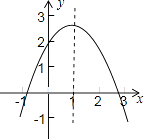
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
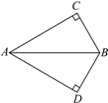
【题目】如图,在△ABC和△ABD中,∠C=∠D=90°,若利用“HL”证明△ABC≌△ABD,则需要添加的条件是________或________.
查看答案和解析>>
科目:初中数学 来源: 题型:
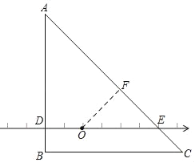
【题目】在同一平面内的图形M,N,给出如下定义:P为图形M上任意一点,Q为图形N上任意一点,如果P,Q两点间的距离有最小值,那么称这个最小值为图形M,N间的“闭距离“,记作d(M,N).
如图,等腰直角三角形ABC的一条直角边AB垂直数轴于点D,斜边AC与数轴交于点E,数轴上点O表示的有理数是0,若AB=BC=8,AD=6,OD=2.点O到边BC的距离与线段DB的长相等.
(1)求d(点O,点E);
(2)求d(点O,△ABC).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂有甲种原料130kg,乙种原料144kg.现用这两种原料生产出A,B两种产品共30件.已知生产每件A产品需甲种原料5kg,乙种原料4kg,且每件A产品可获利700元;生产每件B产品需甲种原料3kg,乙种原料6kg,且每件B产品可获利900元.设生产A产品x件(产品件数为整数件),根据以上信息解答下列问题:
(1)生产A,B两种产品的方案有哪几种;
(2)设生产这30件产品可获利y元,写出y关于x的函数解析式,写出(1)中利润最大的方案,并求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com