
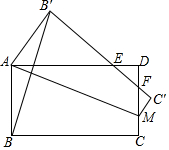
 如图,长方形ABCD中,M为线段CD上一点,将四边形ABCM沿直线AM向上翻折使得点B、C分别落在点B′、C′处,线段B′C′分别交线段AD、CD于点E、F,连接BB′,若∠B′AE+∠BAM=∠AMC,且S△ABB′=2$\sqrt{2}$,则点B′到直线BC的距离为1+$\sqrt{2}$.
如图,长方形ABCD中,M为线段CD上一点,将四边形ABCM沿直线AM向上翻折使得点B、C分别落在点B′、C′处,线段B′C′分别交线段AD、CD于点E、F,连接BB′,若∠B′AE+∠BAM=∠AMC,且S△ABB′=2$\sqrt{2}$,则点B′到直线BC的距离为1+$\sqrt{2}$. 分析 作B′H⊥BC于H,过B′作B′Q⊥BA的延长线于Q,根据翻折的性质得到AB=AB′,AM⊥BB′,进一步得到∠B′AE=45°,设AB′=x,再根据三角函数得到B′Q=$\frac{\sqrt{2}}{2}$x,根据三角形面积公式得到x的值,再由B′H=QB=AQ+AB即可求解.
解答 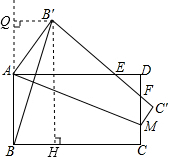 解:作B′H⊥BC于H,过B′作B′Q⊥BA的延长线于Q,
解:作B′H⊥BC于H,过B′作B′Q⊥BA的延长线于Q,
∵AM垂直平分BB′,
∴AB=AB′,AM⊥BB′,
∴∠BAM=∠B′AM,
∴2∠AB′180°-∠BAB′=180°-2∠BAM,
∵∠BAD=90°,
∴∠DAM=∠ABB′=∠AB′B=2α,
∴∠B′AM+∠AB′B=90°,
∴3α+α=90°,
∴2α=45°,
∴∠B′AE=45°,
设AB′=x,则B′Q=$\frac{\sqrt{2}}{2}$x,
∵S△ABB′=2$\sqrt{2}$,
∴$\frac{1}{2}$AB•B′Q=2$\sqrt{2}$,
∴$\frac{1}{2}$x•$\frac{\sqrt{2}}{2}$x=2$\sqrt{2}$,
∴x=$\sqrt{2}$,
∴B′H=QB=AQ+AB=$\frac{\sqrt{2}}{2}$x+x=1+$\sqrt{2}$.
故答案为:1+$\sqrt{2}$.
点评 本题考查了长方形的性质、图形的翻折问题、三角函数、三角形面积,解决本题的关键是求出AB′的长.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:选择题
| A. | (x-$\frac{4+\sqrt{6}}{2}$y)(x-$\frac{4-\sqrt{6}}{2}$y) | B. | 2(x-$\frac{4+\sqrt{6}}{2}$y)(x-$\frac{4-\sqrt{6}}{2}$y) | C. | (2x-4y+$\sqrt{6}$y)(x-$\frac{4-\sqrt{6}}{2}$y) | D. | 2(x-$\frac{4-\sqrt{6}}{2}$y)(x-$\frac{4+\sqrt{6}}{2}$y) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
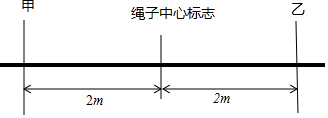 如图,是甲、乙两队同学进行拔河比赛的示意图,绳子的中心标志先向甲方移动0.8m,再向乙方移动1.2m.相持一段时间后,先向乙方移动0.5m,再向甲方移动1.8m,然后向乙方移动0.3m,最后向甲方移动1.6m.若根据规定,绳子的中心标志物从中点处向哪一队的方向移动超过2m.则该队获胜那么现在哪一个队取得了胜利?请通过计算说明你的判断.
如图,是甲、乙两队同学进行拔河比赛的示意图,绳子的中心标志先向甲方移动0.8m,再向乙方移动1.2m.相持一段时间后,先向乙方移动0.5m,再向甲方移动1.8m,然后向乙方移动0.3m,最后向甲方移动1.6m.若根据规定,绳子的中心标志物从中点处向哪一队的方向移动超过2m.则该队获胜那么现在哪一个队取得了胜利?请通过计算说明你的判断.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com