
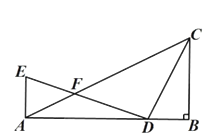
【题目】如图,在△ABC中,∠ABC=90°,D为AB边上一点(BD<BC),AE⊥AB,AE=BD,连接DE交AC于F,若∠AFE=45°,AD=3![]() ,CD=5,则线段AC的长度为_________.
,CD=5,则线段AC的长度为_________.
 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
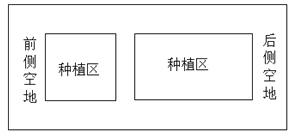
【题目】某村计划建造如图所示的矩形蔬菜温室,要求长宽的比为3:1,在温室内,沿前后两侧的内墙各留2.5m宽的空地放置工具,其他两侧内墙各留1m宽的通道.中间区域再留1m宽的通道,通道与前后墙平行,剩余空地(阴影部分)为种植区,当种植区面积是300m2,求矩形温室的长与宽是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与双曲线
与双曲线![]() 交于第一、三象限内的
交于第一、三象限内的![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,
,![]() ,
,![]() ,点
,点![]() 的纵坐标为4.
的纵坐标为4.

(1)求反比例函数和一次函数的函数表达式;
(2)连接![]() ,求四边形
,求四边形![]() 的面积;
的面积;
(3)在(1)的条件下,根据图像直接写出反比例函数的值小于一次函数的值时,自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料
在数轴上4与![]() 所对的两点之间的距离:
所对的两点之间的距离:![]()
在数轴上![]() 与3所对的两点之间的距离
与3所对的两点之间的距离![]() ;
;
在数轴上![]() 与
与![]() 所对的两点之间的距离:
所对的两点之间的距离:![]() 在数轴上点A、B分别表示数a、b,则A、B两点之间的距离
在数轴上点A、B分别表示数a、b,则A、B两点之间的距离![]()
依据材料知识解答下列问题
![]() 数轴上表示
数轴上表示![]() 和
和![]() 的两点之间的距离是______,数轴上表示数x和3的两点之间的距离表示为______;
的两点之间的距离是______,数轴上表示数x和3的两点之间的距离表示为______;
![]() 七年级研究性学习小组进行如下探究:
七年级研究性学习小组进行如下探究:
![]() 请你在草稿纸上面出数轴当表示数x的点在
请你在草稿纸上面出数轴当表示数x的点在![]() 与2之间移动时,
与2之间移动时,![]() 的值总是一个固定的值为:______,式子
的值总是一个固定的值为:______,式子![]() 的最小值是______.
的最小值是______.
![]() 请你在草稿纸上画出数轴,当x等于______时,
请你在草稿纸上画出数轴,当x等于______时,![]() 的值最小,且最小值是______.
的值最小,且最小值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 一次函数y=﹣2x+3,y随x的增大而减小,
B. 反比例函数![]() 中,y随x的增大而增大,
中,y随x的增大而增大,
C. 抛物线y=x2+1与y=x2﹣1的形状相同,只是位置不同,
D. 二次函数y=﹣2(x﹣2)2+3中,当x>2时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,观察由棱长为 ![]() 的小立方体摆成的图形,寻找规律:如图 ① 中,共有
的小立方体摆成的图形,寻找规律:如图 ① 中,共有 ![]() 个小立方体,其中
个小立方体,其中 ![]() 个看得见,
个看得见, ![]() 个看不见;如图 ② 中,共有
个看不见;如图 ② 中,共有 ![]() 个小立方体,其中
个小立方体,其中 ![]() 个看得见,
个看得见, ![]() 个看不见;如图 ③ 中,共有
个看不见;如图 ③ 中,共有 ![]() 个小立方体,其中
个小立方体,其中 ![]() 个看得见,
个看得见, ![]() 个看不见;
个看不见; ![]() ,则第 ⑥个图中,看得见的小立方体有________________个.
,则第 ⑥个图中,看得见的小立方体有________________个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE.
(1)求证:△AGE≌△BGF;
(2)试判断四边形AFBE的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育老师对九年级(9)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如下所示:
组别 | 次数x | 频数(人数) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 | a |
第4组 | 140≤x<160 | 18 |
第5组 | 160≤x<180 | 6 |

请结合图表完成下列问题:
(1)表中的a=________;
(2)请把频数分布直方图补充完整;
(3)这个样本数据的中位数落在第________组;
(4)若九年级学生一分钟跳绳次数(x)达标要求是:x<120为不合格;120≤x<140,为合格;140≤x<160为良;x≥160为优.根据以上信息,请你给学校或九年级同学提一条合理化建议:_________________________________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,D是等边△ABC的边BA上一动点(点D与点B不重合),连接DC,以DC为边,在BC上方作等边△DCF,连接AF,你能发现AF与BD之间的数量关系吗?并证明你发现的结论;
(2)如图②,当动点D运动至等边△ABC边BA的延长线时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?若成立,请证明;
(3)Ⅰ.如图③,当动点D在等边△ABC边BA上运动时(点D与B不重合),连接DC,以DC为边在BC上方和下方分别作等边△DCF和等边△DCF′,连接AF,BF′,探究AF,BF′与AB有何数量关系?并证明你的探究的结论;
Ⅱ.如图④,当动点D在等边△ABC的边BA的延长线上运动时,其他作法与图③相同,Ⅰ中的结论是否成立?若不成立,是否有新的结论?并证明你得出的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com