
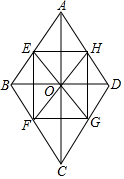
 已知菱形ABCD的对角线相交于O,点E、F分别在边AB、BC上,且BE=BF,射线EO、FO分别交边CD、AD于G、H.
已知菱形ABCD的对角线相交于O,点E、F分别在边AB、BC上,且BE=BF,射线EO、FO分别交边CD、AD于G、H.分析 (1)先根据对角线互相平分证明四边形EFGH是平行四边形,再证明△EBO≌△FBO,得EG=FH,所以四边形EFGH是矩形;
(2)根据垂线段最短,可知:当OE⊥AB时,OE最小,先利用面积法求OE的长,EG=2OE,可得结论.
解答 证明:(1)∵四边形ABCD是菱形,
∴OA=OC,OB=OD,AB∥CD,AD∥BC,
∴∠BAO=∠DCO,∠AOE=∠GOC,
∴△AOE≌△COG(ASA),
∴OE=OG,
同理得:OH=OF,
∴四边形EFGH是平行四边形,
∵BE=BF,∠ABD=∠CBD,OB=OB,
∴△EBO≌△FBO,
∴OE=OF,
∴EG=FH,
∴四边形EFGH是矩形;
(2)∵垂线段最短,
∴当OE⊥AB时,OE最小,
∵OA=4,OB=3,∠AOB=90°,
∴AB2=OA2+OB2=25,
∴AB=5,
∴$\frac{1}{2}$OA×OB=$\frac{1}{2}$AB×OE,
3×4=5×OE,
OE=$\frac{12}{5}$,
∵OE=OG,
∴EG=$\frac{24}{5}$.
答:EG的最小值是$\frac{24}{5}$.
点评 本题考查了菱形的性质、矩形的性质和判定、三角形全等的性质和判定、勾股定理,熟练掌握矩形的判定是关键,同时还运用了面积法求线段OE的长.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:解答题
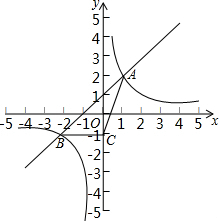 如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=x+b的图象交于A,B两点,点A和点B的横坐标分别为1和-2,这两点的纵坐标之和为1.
如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=x+b的图象交于A,B两点,点A和点B的横坐标分别为1和-2,这两点的纵坐标之和为1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
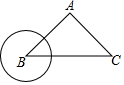 如图,△ABC中,AB=AC=5,BC=8,⊙B的半径为2,圆心B从点B出发,沿着线段BC向右平移,⊙B随着点B的平移而以相同的速度平移.当⊙B与边AB相切时,⊙B平移的距离是$\frac{10}{3}$.
如图,△ABC中,AB=AC=5,BC=8,⊙B的半径为2,圆心B从点B出发,沿着线段BC向右平移,⊙B随着点B的平移而以相同的速度平移.当⊙B与边AB相切时,⊙B平移的距离是$\frac{10}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在直角坐标系中,第一次将△OAB变换成△O1A1B1,第二次将△O1A1B1变换成△O2A2B2,第三次将△O2A2B2变换成△O3A3B3.已知A(1,4),A1(2,4),A2(4,4),A3(8,4),B(2,0),B1(4,0),B2(8,0),B3(16,0).
如图,在直角坐标系中,第一次将△OAB变换成△O1A1B1,第二次将△O1A1B1变换成△O2A2B2,第三次将△O2A2B2变换成△O3A3B3.已知A(1,4),A1(2,4),A2(4,4),A3(8,4),B(2,0),B1(4,0),B2(8,0),B3(16,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
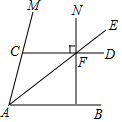 如图,AB∥CD,AE平分∠MAB交CD于点F,NF⊥CD,垂足为点F.
如图,AB∥CD,AE平分∠MAB交CD于点F,NF⊥CD,垂足为点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
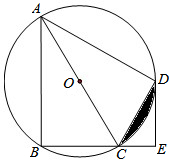 如图,四边形ABCD是⊙O的内接四边形,AC为直径,$\widehat{BD}$=$\widehat{AD}$,DE⊥BC,垂足为E.
如图,四边形ABCD是⊙O的内接四边形,AC为直径,$\widehat{BD}$=$\widehat{AD}$,DE⊥BC,垂足为E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在菱形ABCD中,∠BAD=135°,AB=4$\sqrt{2}$,点P是菱形ABCD内或边上的一点,且∠DAP+∠CBP=90°,连接DP,CP,则△DCP面积的最小值为8$\sqrt{2}$-8.
如图,在菱形ABCD中,∠BAD=135°,AB=4$\sqrt{2}$,点P是菱形ABCD内或边上的一点,且∠DAP+∠CBP=90°,连接DP,CP,则△DCP面积的最小值为8$\sqrt{2}$-8.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 8 | C. | 2 | D. | $\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com