
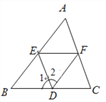
【题目】如图,(1)如果∠1=__________,那么DE∥AC;(同位角相等,两直线平行);
(2)如果∠1=__________,那么EF∥BC;(内错角相等,两直线平行);
(3)如果∠DEF+__________=180°,那么DE∥AC;(同旁内角互补,两直线平行);
(4)如果∠2+__________=180°,那么AB∥DF;(同旁内角互补,两直线平行).
科目:初中数学 来源: 题型:
【题目】(10分)问题:如图(1),在Rt△ACB中,∠ACB=90°,AC=CB,∠DCE=45°,试探究AD、DE、EB满足的等量关系.

[探究发现]
小聪同学利用图形变换,将△CAD绕点C逆时针旋转90°得到△CBH,连接EH,由已知条件易得∠EBH=90°,∠ECH=∠ECB+∠BCH=∠ECB+∠ACD=45°.根据“边角边”,可证△CEH≌ ,得EH=ED.
在Rt△HBE中,由 定理,可得BH2+EB2=EH2,由BH=AD,可得AD、DE、EB之间的等量关系是 .
[实践运用]
(1)如图(2),在正方形ABCD中,△AEF的顶点E、F分别在BC、CD边上,高AG与正方形的边长相等,求∠EAF的度数;
(2)在(1)条件下,连接BD,分别交AE、AF于点M、N,若BE=2,DF=3,BM=2![]() ,运用小聪同学探究的结论,求正方形的边长及MN的长.
,运用小聪同学探究的结论,求正方形的边长及MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB的垂直平分线CP交AB于点P,且AP=2PC,现欲在线段AB上求作两点D,E,使其满足AD=DC=CE=EB,对于以下甲、乙两种作法:
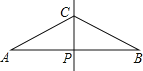
甲:分别作∠ACP、∠BCP的平分线,分别交AB于D、E,则D、E即为所求;乙:分别作AC、BC的垂直平分线,分别交AB于D、E,则D、E两点即为所求.下列说法正确的是( )
A. 甲、乙都正确 B. 甲、乙都错误
C. 甲正确,乙错误 D. 甲错误,乙正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育委员统计了全班同学60秒跳绳的次数,并列出下面的频数分布表:
次数 | 60≤x<90 | 90≤x<120 | 120≤x<150 | 150≤x<180 | 180≤x<210 |
频数 | 16 | 25 | 9 | 7 | 3 |
(1)全班有多少同学?
(2)组距是多少?组数是多少?
(3)跳绳次数x在120≤x<180范围的同学有多少?占全班同学的百分之几(精确到0.1%)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A.同一条弦所对的两条弧一定是等弧
B.长度相等的两条弧是等弧
C.正多边形一定是轴对称图形
D.三角形的外心到三角形各边的距离相等
查看答案和解析>>
科目:初中数学 来源: 题型:
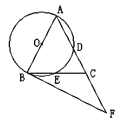
【题目】如图,在△ABC中,AB=AC,∠BAC=54°,以AB为直径的 ⊙O分别交AC,BC于点D,E,过点B作⊙O的切线,交AC的延长线于点F.
(1)求证:BE=CE;
(2)求∠CBF的度数;
(3)若AB=6,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1=65°,∠2=65°,∠3=115°.试说明:DE∥BC,DF∥AB.根据图形,完成下面的推理:
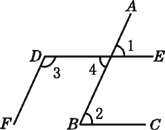
因为∠1=65°,∠2=65°,
所以∠1=∠2.
所以______________∥ ( ).
因为AB与DE相交,
所以∠1=∠4( ).
所以∠4=65°.
又因为∠3=115°,
所以∠3+∠4=180°.
所以 ∥ ( ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com