
分析 先得出a=-b或b=-c或c=-a,分三种情况代换,化简即可得出结论.
解答 解:∵三个不等于零的有理数a,b,c满足(a+b)(b+c)(c+a)=0,∴a+b=0或b+c=0或c+a=0,∴a=-b或b=-c或c=-a,
当a=-b时,a+b+b=-b+b+c=c,
a3+b3+c3=(-b)3+b3+c3=-b3+b3+c3=c3,
a5+b5+c5=(-b)5+b5+c5=-b5+b5+c5=c5,
a9+b9+c9=(-b)9+b9+c9=-b9+b9+c9=c9,
a25+b25+c25=(-b)25+b25+c25=-b25+b25+c25=c25
∴$\frac{(a+b+c)({a}^{3}+{b}^{3}+{c}^{3})({a}^{5}+{b}^{5}+{c}^{5})({a}^{7}+{b}^{7}+{c}^{7})({a}^{9}+{b}^{9}+{c}^{9})}{{a}^{25}+{b}^{25}+{c}^{25}}$=$\frac{c×{c}^{3}×{c}^{5}×{c}^{7}×{c}^{9}}{{c}^{25}}$=$\frac{{c}^{1+3+5+7+9}}{{c}^{25}}$=$\frac{{c}^{25}}{{c}^{25}}$=1,
同理:当b=-c时或当c=-a时,则$\frac{(a+b+c)({a}^{3}+{b}^{3}+{c}^{3})({a}^{5}+{b}^{5}+{c}^{5})({a}^{7}+{b}^{7}+{c}^{7})({a}^{9}+{b}^{9}+{c}^{9})}{{a}^{25}+{b}^{25}+{c}^{25}}$=1,
即:则$\frac{(a+b+c)({a}^{3}+{b}^{3}+{c}^{3})({a}^{5}+{b}^{5}+{c}^{5})({a}^{7}+{b}^{7}+{c}^{7})({a}^{9}+{b}^{9}+{c}^{9})}{{a}^{25}+{b}^{25}+{c}^{25}}$=1,
故答案为1.
点评 此题主要考查了幂的乘方,积的次方,同底数幂的乘法,解本题的关键是得出a=-b或b=-c或c=-a,是一道很好的基础题.


科目:初中数学 来源: 题型:解答题
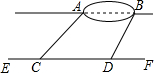 某兴趣小组想测量位于一池塘两端的A、B之间的距离,组长小明带领小组成员沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到达点D处,测得∠BDF=60°,已知AB与EF之间的距离为60米,求A、B两点的距离.
某兴趣小组想测量位于一池塘两端的A、B之间的距离,组长小明带领小组成员沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到达点D处,测得∠BDF=60°,已知AB与EF之间的距离为60米,求A、B两点的距离.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
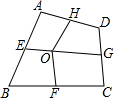 如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若S四边形AEOH=4,S四边形BFOE=5,S四边形CGOF=6,则S四边形DHOG为( )
如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若S四边形AEOH=4,S四边形BFOE=5,S四边形CGOF=6,则S四边形DHOG为( )| A. | 3 | B. | 5 | C. | 7 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
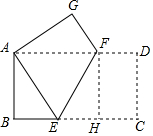 如图,将长方形ABCD沿直线EF折叠,使顶点C恰好落在顶点A处,已知AB=4cm,AD=8cm,则折痕EF的长为( )
如图,将长方形ABCD沿直线EF折叠,使顶点C恰好落在顶点A处,已知AB=4cm,AD=8cm,则折痕EF的长为( )| A. | 5cm | B. | $2\sqrt{5}$cm | C. | 2$\sqrt{3}$cm | D. | $3\sqrt{5}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方形ABCD中,E为BC的中点,CG⊥DE于G,BG延长交CD于点F,CG延长交BD于点H,AB于N.下列结论:①DE=CN;②∠DGF=45°;③2BN=3CF;④CH+BH=DE.其中正确的有( )
如图,正方形ABCD中,E为BC的中点,CG⊥DE于G,BG延长交CD于点F,CG延长交BD于点H,AB于N.下列结论:①DE=CN;②∠DGF=45°;③2BN=3CF;④CH+BH=DE.其中正确的有( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
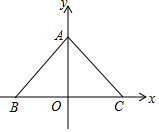 如图,坐标平面上有A(0,a)、B(-9,0)、C(10,0)点,其中a>0,若∠BAC=100°,则△ABC的外心在( )
如图,坐标平面上有A(0,a)、B(-9,0)、C(10,0)点,其中a>0,若∠BAC=100°,则△ABC的外心在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com