
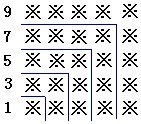
 探索规律:观察下面由※组成的图案和算式,解答问题:
探索规律:观察下面由※组成的图案和算式,解答问题:分析 (1)根据已知得出连续奇数的和等于数字个数的平方;
(2)根据已知得出连续奇数的和等于数字个数的平方,得出答案即可;
(3)利用以上已知条件得出51+53+55+…+2011+2013=(1+3+5+…+2007+2013)-(1+3+5+…+49),求出即可.
解答 解:(1)由已知得出:
1+3=4=22
1+3+5=9=32
1+3+5+7=19=42
1+3+5+7+9=25=52
依此类推:第n个所代表的算式为:1+3+5+…+(2n-1)=n2;
(1)当2n-1=19,即n=10时,1+3+5+…+19=102.
(2)($\frac{2n+3+1}{2}$)2=(n+2)2;
(3)51+53+55+…+2011+2013
03+105+107+…+2007+2009,
=(1+3+5+…+2011+2013)-(1+3+5+…+49)
=($\frac{2013+1}{2}$)2-($\frac{49+1}{2}$)2=10052-512
=10072-252
=1003104.
故答案为:100,(n+2)2.
点评 此题主要考查了数字变化规律,培养学生通过特例分析从而归纳总结出一般结论的能力.通过分析找到各部分的变化规律后用一个统一的式子表示出变化规律是此类题目的难点.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:解答题
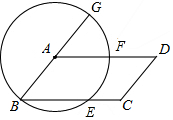 如图,以□ABCD的顶点A为圆心,AB为半径作⊙A,分别交BC,AD于E,F两点,交BA的延长线于G,判断$\widehat{EF}$和$\widehat{FG}$是否相等,并说明理由.
如图,以□ABCD的顶点A为圆心,AB为半径作⊙A,分别交BC,AD于E,F两点,交BA的延长线于G,判断$\widehat{EF}$和$\widehat{FG}$是否相等,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
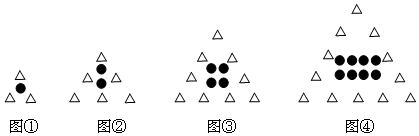
| A. | 88 | B. | 91 | C. | 152 | D. | 155 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com