
���� ��1���ȸ��ݷ�ʽ�������ķ����ԭʽ���л��������x��ֵ������м��㼴�ɣ�
��2����������⡿��x=4k��y=3k��z=2k������м��㼴�ɣ�
����չӦ�á���$\frac{x}{3}$=-$\frac{y}{2}$=$\frac{z}{4}$=k����x=3k��y=-2k��z=4k���ٴ����ʽ���м��㼴�ɣ�
��� �⣺��1��ԭʽ=$\frac{1}{x}$��$\frac{{x}^{2}+1-2x}{x��x-1��}$+$\frac{1}{x+1}$
=$\frac{1}{x}$��$\frac{��x-1��^{2}}{x��x-1��}$+$\frac{1}{x+1}$
=$\frac{1}{x}$��$\frac{x-1}{x}$+$\frac{1}{x+1}$
=$\frac{1}{x}$•$\frac{x}{x-1}$+$\frac{1}{x+1}$
=$\frac{1}{x-1}$+$\frac{1}{x+1}$
=$\frac{x+1+x-1}{��x-1����x+1��}$
=$\frac{2x}{��x-1����x+1��}$��
��x=2-1-20160=$\frac{1}{2}$-1=-$\frac{1}{2}$ʱ��ԭʽ=$\frac{2����-\frac{1}{2}��}{��-\frac{1}{2}-1����-\frac{1}{2}+1��}$=$\frac{-1}{��-\frac{3}{2}����\frac{1}{2}}$=$\frac{4}{3}$��
��2����������⡿��x=4k��y=3k��z=2k����ã�
ԭʽ=$\frac{16{k}^{2}+9{k}^{2}}{12{k}^{2}-8{k}^{2}}$=$\frac{25{k}^{2}}{4{k}^{2}}$=$\frac{25}{4}$��
�ʴ�Ϊ��$\frac{25}{4}$��
����չӦ�á���$\frac{x}{3}$=-$\frac{y}{2}$=$\frac{z}{4}$=k����x=3k��y=-2k��z=4k��
ԭʽ=$\frac{��x-y��^{2}}{��y+2z��^{2}}$=$\frac{��3k+2k��^{2}}{��-2k+8k��^{2}}$=$\frac{25{k}^{2}}{36{k}^{2}}$=$\frac{25}{36}$��
���� ���⿼����Ƿ�ʽ�Ļ�����ֵ���ڽ�������ĿʱҪע�⣬������������ʽ����˿���������������������k���ó�x��y��z��k�Ĺ�ϵ��Ȼ���ٴ������ķ�ʽ���ɣ�


 ��һ����ͬ���ɽ�����ϵ�д�
��һ����ͬ���ɽ�����ϵ�д� ������Ӧ���ϵ�д�
������Ӧ���ϵ�д� ��ʦ�㾦�ִʾ��ƪϵ�д�
��ʦ�㾦�ִʾ��ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����A��B��C��DΪ��O�ϵ��ĸ��㣬$\widehat{BC}$=$\widehat{CD}$��AC��BD�ڵ�E��CE=4��CD=6��
��ͼ����A��B��C��DΪ��O�ϵ��ĸ��㣬$\widehat{BC}$=$\widehat{CD}$��AC��BD�ڵ�E��CE=4��CD=6���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\left\{\begin{array}{l}{x=2}\\{y=2}\\{z=1}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{x=2}\\{y=1}\\{z=1}\end{array}\right.$ | C�� | $\left\{\begin{array}{l}{x=-2}\\{y=8}\\{z=1}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{x=2}\\{y=2}\\{z=2}\end{array}\right.$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
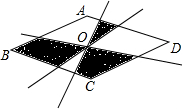 ��ͼ���ı���ABCD�����Σ���O�ǶԽ��ߵĽ��㣬����ֱ�߶�������O��ͼ����Ӱ���Ϊ24cm2������һ�ԶԽ��߳�Ϊ6cm������һ���Խ��߳�Ϊ16cm��
��ͼ���ı���ABCD�����Σ���O�ǶԽ��ߵĽ��㣬����ֱ�߶�������O��ͼ����Ӱ���Ϊ24cm2������һ�ԶԽ��߳�Ϊ6cm������һ���Խ��߳�Ϊ16cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
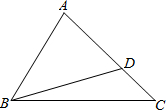 ��ͼ����ABC�У���C=45�㣬��D��AC�ϣ��ҡ�ADB=60�㣬ABΪ��BCD���Բ�����ߣ�
��ͼ����ABC�У���C=45�㣬��D��AC�ϣ��ҡ�ADB=60�㣬ABΪ��BCD���Բ�����ߣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ڡ�O���ڽ��ı���ABCD�У�AB��ֱ������BCD=120�㣬����D������PD��ֱ��AB���ڵ�P����sin��ADP��ֵΪ��������
��ͼ���ڡ�O���ڽ��ı���ABCD�У�AB��ֱ������BCD=120�㣬����D������PD��ֱ��AB���ڵ�P����sin��ADP��ֵΪ��������| A�� | $\frac{\sqrt{3}}{3}$ | B�� | $\frac{\sqrt{3}}{2}$ | C�� | $\frac{\sqrt{2}}{2}$ | D�� | $\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com