
ΓΨΧβΡΩΓΩ‘ΤΡœ¬≥Βι6.5ΦΕΒΊ’πΚσΘ§Ω’ΨϋΡ≥≤ΩΖνΟϋΗΑ‘÷«χΩ’ΆΕΨ»‘÷ΈοΉ Θ§“―÷ΣΈοΉ άκΩΣΖ…Μζ‘ΎΩ’÷–―Ί≈ΉΈοœΏΫΒ¬δΘ§≈ΉΈοœΏΒΡΕΞΒψ‘ΎΜζ≤’≤’ΩΎΒψA¥Π(»γΆΦΥυ Ψ).
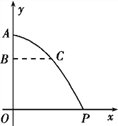
(1)»τΈοΧεάκΩΣA¥ΠΚσœ¬¬δΒΡ ζ÷±ΗΏΕ»AB=160 m ±Θ§Υ°ΤΫΨύάκBC=200 mΘ§Ρ«Ο¥“Σ ΙΖ…Μζ‘Ύ ζ÷±ΗΏΕ»OA=1 kmΒΡΩ’÷–Ω’ΆΕΒΡΈοΉ «ΓΚΟ¬δ‘ΎΨ”ΟώΒψP¥ΠΘ§«σΖ…ΜζΒΫΒψP¥ΠΒΡΥ°ΤΫΨύάκOP”ΠΈΣΕύ…ΌΘΜ
(2)ΗυΨίΒ± ±ΒΡΖγΝΠ≤βΥψΘ§Ω’ΆΕΈοΉ άκΩΣA¥ΠΒΡ ζ÷±ΨύάκΈΣ160 m ±Θ§ΥϋΒΫA¥ΠΒΡΥ°ΤΫΨύάκΫΪ‘ω÷Ν400 m.“Σ ΙΖ…Μζ‘Ύ(1)÷–ΒΡΒψO’ΐ…œΖΫΩ’ΆΕΈοΉ ΒΫP¥ΠΘ§Ζ…ΜζάκΒΊΟφΒΡΗΏΕ»”ΠΈΣΕύ…Ό?
ΓΨ¥πΑΗΓΩΘ®1Θ©Ζ…ΜζΒΫP¥ΠΒΡΥ°ΤΫΨύάκOP”ΠΈΣ500 mΘΜΘ®2Θ©Ζ…ΜζάκΒΊΟφΒΡΗΏΕ»”ΠΈΣ250 m.
ΓΨΫβΈωΓΩ(1)ΗυΨί¥ΐΕ®œΒ ΐΖ®,Ω…ΒΟΚ· ΐΫβΈω Ϋ,ΗυΨίΚ· ΐ÷Β,Ω…ΒΟœύ”ΠΉ‘±δΝΩΒΡ÷Β;
(2)ΗυΨί¥ΐΕ®œΒ ΐΖ®,Ω…ΒΟΚ· ΐΫβΈω Ϋ,ΗυΨίΉ‘±δΝΩΒΡ÷Β,Ω…ΒΟœύ”ΠΒΡΚ· ΐ÷Β.
(1)”…Χβ“β÷ΣΘ§≈ΉΈοœΏΒΡΕΞΒψΉχ±ξΈΣ(0Θ§1 000)Θ§ΓΏAB=160 mΘ§BC=200 mΘ§
ΓύΒψCΒΡΉχ±ξΈΣ(200Θ§840).
…η≈ΉΈοœΏΒΡΚ· ΐ±μ¥ο ΫΈΣy=ax2+1 000(aΓΌ0).
ΓΏΒψC(200Θ§840)‘Ύ≈ΉΈοœΏ…œΘ§
Γύ840=aΓΝ2002+1 000Θ§
ΫβΒΟa=-![]() .
.
Γύ≈ΉΈοœΏΒΡΚ· ΐ±μ¥ο ΫΈΣy=-![]() x2+1 000.
x2+1 000.
Β±y=0 ±Θ§-![]() x2+1 000=0Θ§
x2+1 000=0Θ§
ΫβΒΟx1=500Θ§x2=-500(…α»Ξ).
ΓύΖ…ΜζΒΫP¥ΠΒΡΥ°ΤΫΨύάκOP”ΠΈΣ500 m.
(2)…ηΖ…ΜζάκΒΊΟφΒΡΗΏΕ»ΈΣk mΘ§≈ΉΈοœΏΒΡΚ· ΐ±μ¥ο ΫΈΣy=a'x2+k(a'ΓΌ0).
”…Χβ“β÷ΣΘ§ΒψC'(400Θ§k-160)‘Ύ≈ΉΈοœΏ…œΘ§
Γύk-160=a'ΓΝ4002+k.
ΫβΒΟa'=-![]() .
.
Γύ¥Υ ±≈ΉΈοœΏΒΡΚ· ΐ±μ¥ο ΫΈΣy=-![]() x2+k.
x2+k.
ΓΏΒ±x=500 ±Θ§y=0Θ§
Γύ-![]() ΓΝ5002+k=0Θ§ΫβΒΟk=250.
ΓΝ5002+k=0Θ§ΫβΒΟk=250.
ΓύΖ…ΜζάκΒΊΟφΒΡΗΏΕ»”ΠΈΣ250 m.


 Οϊ≈Τ―ß–ΘΖ÷≤ψ÷ή÷ή≤βœΒΝ–¥πΑΗ
Οϊ≈Τ―ß–ΘΖ÷≤ψ÷ή÷ή≤βœΒΝ–¥πΑΗ ΜΤΗ‘ΚΘΒμ»Ϊ≥Χ≈ύ”≈≤β ‘ΨμœΒΝ–¥πΑΗ
ΜΤΗ‘ΚΘΒμ»Ϊ≥Χ≈ύ”≈≤β ‘ΨμœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦ1 «±Ώ≥ΛΈΣ![]() ΒΡ’ΐΖΫ–Έ±ΓΧζΤ§Θ§–ΓΟςΫΪΤδΥΡΫ«ΗςΦτ»Ξ“ΜΗωœύΆ§ΒΡ–Γ’ΐΖΫ–ΈΘ®ΆΦ÷–“θ”Α≤ΩΖ÷Θ©ΚσΘ§ΖΔœ÷ Θ”ύΒΡ≤ΩΖ÷Ρή’έ≥…“ΜΗωΈόΗ«ΒΡ≥ΛΖΫΧεΚ–Ή”Θ§ΆΦ2ΈΣΚ–Ή”ΒΡ Ψ“βΆΦΘ®ΧζΤ§ΒΡΚώΕ»Κω¬‘≤ΜΦΤΘ©Θ°
ΒΡ’ΐΖΫ–Έ±ΓΧζΤ§Θ§–ΓΟςΫΪΤδΥΡΫ«ΗςΦτ»Ξ“ΜΗωœύΆ§ΒΡ–Γ’ΐΖΫ–ΈΘ®ΆΦ÷–“θ”Α≤ΩΖ÷Θ©ΚσΘ§ΖΔœ÷ Θ”ύΒΡ≤ΩΖ÷Ρή’έ≥…“ΜΗωΈόΗ«ΒΡ≥ΛΖΫΧεΚ–Ή”Θ§ΆΦ2ΈΣΚ–Ή”ΒΡ Ψ“βΆΦΘ®ΧζΤ§ΒΡΚώΕ»Κω¬‘≤ΜΦΤΘ©Θ°
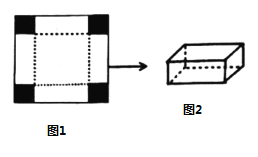
Θ®1Θ©…ηΦτ»ΞΒΡ–Γ’ΐΖΫ–ΈΒΡ±Ώ≥ΛΈΣ![]() Θ§’έ≥…ΒΡ≥ΛΖΫΧεΚ–Ή”ΒΡ»ίΜΐΈΣ
Θ§’έ≥…ΒΡ≥ΛΖΫΧεΚ–Ή”ΒΡ»ίΜΐΈΣ![]() Θ§÷±Ϋ”–¥≥ω”Ο÷ΜΚ§Ή÷ΡΗ
Θ§÷±Ϋ”–¥≥ω”Ο÷ΜΚ§Ή÷ΡΗ![]() ΒΡ ΫΉ”±μ Ψ’βΗωΚ–Ή”ΒΡΗΏΈΣ______
ΒΡ ΫΉ”±μ Ψ’βΗωΚ–Ή”ΒΡΗΏΈΣ______![]() Θ§ΒΉΟφΜΐΈΣ______
Θ§ΒΉΟφΜΐΈΣ______![]() Θ§Κ–Ή”ΒΡ»ίΜΐ
Θ§Κ–Ή”ΒΡ»ίΜΐ![]() ΈΣ______
ΈΣ______![]() Θ§
Θ§
Θ®2Θ©ΈΣΧΫΨΩΚ–Ή”ΒΡΧεΜΐ”κΦτ»ΞΒΡ–Γ’ΐΖΫ–ΈΒΡ±Ώ≥Λ![]() ÷°ΦδΒΡΙΊœΒΘ§–ΓΟςΝ–±μ
÷°ΦδΒΡΙΊœΒΘ§–ΓΟςΝ–±μ
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 324 |
| 588 | 576 | 500 |
| 252 | 128 |
ΧνΩ’ΘΚΔΌ![]() ______Θ§
______Θ§![]() ______ΘΜ
______ΘΜ
ΔΎ”…±μΗώ÷–ΒΡ ΐΨίΙέ≤λΩ…÷ΣΒ±![]() ΒΡ÷Β÷πΫΞ‘ω¥σ ±Θ§
ΒΡ÷Β÷πΫΞ‘ω¥σ ±Θ§![]() ΒΡ÷Β______Θ°Θ®¥”ΓΑ÷πΫΞ‘ω¥σΓ±Θ§ΓΑ÷πΫΞΦθ–ΓΓ±ΓΑœ»‘ω¥σΚσΦθ–ΓΓ±Θ§ΓΑœ»Φθ–ΓΚσ‘ω¥σΓ±÷–―Γ“ΜΗωΫχ––ΧνΩ’Θ©
ΒΡ÷Β______Θ°Θ®¥”ΓΑ÷πΫΞ‘ω¥σΓ±Θ§ΓΑ÷πΫΞΦθ–ΓΓ±ΓΑœ»‘ω¥σΚσΦθ–ΓΓ±Θ§ΓΑœ»Φθ–ΓΚσ‘ω¥σΓ±÷–―Γ“ΜΗωΫχ––ΧνΩ’Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΨΊ–Έ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() œύΫΜ”ΎΒψ
œύΫΜ”ΎΒψ![]() Θ§
Θ§![]() ΤΫΖ÷
ΤΫΖ÷![]() ΫΜ
ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§»τ
Θ§»τ![]() Θ§‘ρ
Θ§‘ρ![]() ________Θ°
________Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
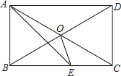
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΫΉΧίΆΦΒΡΟΩΗωΧ®ΫΉ…œΕΦ±ξΉ≈“ΜΗω ΐΘ§ ¥”œ¬ΒΫ…œΒΡΒΎ![]() Ηω÷ΝΒΎ
Ηω÷ΝΒΎ![]() ΗωΧ®ΫΉ…œ“ά¥Έ±ξΉ≈
ΗωΧ®ΫΉ…œ“ά¥Έ±ξΉ≈![]() Θ§«“»Έ“βœύΝΎΥΡΗωΧ®ΫΉ…œΒΡ ΐΒΡΚΆΕΦœύΒ»Θ°
Θ§«“»Έ“βœύΝΎΥΡΗωΧ®ΫΉ…œΒΡ ΐΒΡΚΆΕΦœύΒ»Θ°

![]() «σ«Α
«σ«Α![]() ΗωΧ®ΫΉ…œΒΡ ΐΒΡΚΆΘΜ
ΗωΧ®ΫΉ…œΒΡ ΐΒΡΚΆΘΜ
![]() «σΒΎ
«σΒΎ![]() ΗωΧ®ΫΉ…œΒΡ ΐxΒΡ÷ΒΘΜ
ΗωΧ®ΫΉ…œΒΡ ΐxΒΡ÷ΒΘΜ
![]() ¥”œ¬ΒΫ…œ«Α
¥”œ¬ΒΫ…œ«Α![]() ΈΣΤφ ΐ)ΗωΧ®ΫΉ…œΒΡ ΐΒΡΚΆΡήΖώΈΣ
ΈΣΤφ ΐ)ΗωΧ®ΫΉ…œΒΡ ΐΒΡΚΆΡήΖώΈΣ![]() ΘΩ»τΡήΘ§«σ≥ω
ΘΩ»τΡήΘ§«σ≥ω![]() ΒΡ÷ΒΘΜ»τ≤ΜΡήΘ§«κΥΒΟςάμ”…Θ°
ΒΡ÷ΒΘΜ»τ≤ΜΡήΘ§«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Υ≥« –Ε‘ –ΟώΩΣ’ΙΝΥ”–ΙΊΈμω≤ΒΡΒς≤ιΈ ΨμΘ§Βς≤ιΡΎ»ί «ΓΑΡψ»œΈΣΡΡ÷÷¥κ ©÷ΈάμΈμω≤Ήν”––ßΓ±Θ§”–“‘œ¬ΥΡΗω―ΓœνΘΚ
AΘ°¬ΧΜ·‘λΝ÷ BΘ°Τϊ≥Βœό–– CΘ°≤π≥ΐ»ΦΟΚ–ΓΙχ¬· ΓΓΓΓDΘ° Ι”Ο«εΫύΡή‘¥Θ°
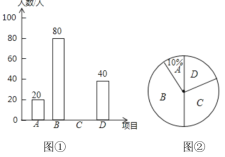
Βς≤ιΙΐ≥ΧΥφΜζ≥ι»ΓΝΥ≤ΩΖ÷ –ΟώΫχ––Βς≤ιΘ§≤ΔΫΪΒς≤ιΫαΙϊΜφ÷ΤΝΥΝΫΖυ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΘ§«κΜΊ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©’β¥Έ±ΜΒς≤ιΒΡ –ΟώΙ≤”–Εύ…Ό»ΥΘΩ
Θ®2Θ©«κΡψΫΪΆ≥ΦΤΆΦ1≤Ι≥δΆξ’ϊΘ°
Θ®3Θ©«σΆΦ2÷–![]() œνΡΩΕ‘”ΠΒΡ…»–ΈΒΡ‘≤–ΡΫ«ΒΡΕ» ΐΘ°
œνΡΩΕ‘”ΠΒΡ…»–ΈΒΡ‘≤–ΡΫ«ΒΡΕ» ΐΘ°
Θ®4Θ©«κΡψΫαΚœΉ‘ΦΚΒΡ ΒΦ «ιΩωΕ‘”––ß÷ΈάμΈμω≤ΧαΦΗΒψΫ®“ιΘ°Θ®÷Ν…Ό–¥“ΜΧθΘ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΧΫΨΩ÷ΛΟςΘΚ
Θ®1Θ©»γΆΦ1Θ§‘ΎΓςABC÷–Θ§AB=ACΘ§ΒψE «BC…œΒΡ“ΜΗωΕ·ΒψΘ§EGΓΆABΘ§EFΓΆACΘ§CDΓΆABΘ§ΒψGΘ§FΘ§DΖ÷±π «¥ΙΉψΘ°«σ÷ΛΘΚCD=EG+EFΘΜ
≤¬œκΧΫΨΩΘΚ
Θ®2Θ©»γΆΦ2Θ§‘ΎΓςABC÷–Θ§AB=ACΘ§ΒψE «BCΒΡ―”≥ΛœΏ…œΒΡ“ΜΗωΕ·ΒψΘ§EGΓΆAB”ΎGΘ§EFΓΆACΫΜAC―”≥ΛœΏ”ΎFΘ§CDΓΆAB”ΎDΘ§÷±Ϋ”≤¬œκCDΓΔEGΓΔEF÷°ΦδΒΡΙΊœΒΈΣ CD=EG©¹EF ΘΜ
Έ ΧβΫβΨωΘΚ
Θ®3Θ©»γΆΦ3Θ§±Ώ≥ΛΈΣ10ΒΡ’ΐΖΫ–ΈABCDΒΡΕ‘Ϋ«œΏœύΫΜ”ΎΒψOΓΔH‘ΎBD…œΘ§«“BH=BCΘ§Ν§Ϋ”CHΘ§ΒψE «CH…œ“ΜΒψΘ§EFΓΆBD”ΎΒψFΘ§EGΓΆBC”ΎΒψGΘ§‘ρEF+EG= Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
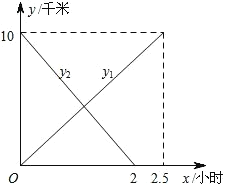
ΓΨΧβΡΩΓΩΡ≥÷–―ßΨ≈ΡξΦΕΦΉΓΔ““ΝΫΑύ…ΧΕ®ΨΌ––“Μ¥Έ‘ΕΉψΜνΕ·Θ§![]() ΓΔ
ΓΔ![]() ΝΫΒΊœύΨύ10«ßΟΉΘ§ΦΉΑύ¥”
ΝΫΒΊœύΨύ10«ßΟΉΘ§ΦΉΑύ¥”![]() ΒΊ≥ωΖΔ‘»ΥΌ≤Ϋ––ΒΫ
ΒΊ≥ωΖΔ‘»ΥΌ≤Ϋ––ΒΫ![]() ΒΊΘ§““Αύ¥”
ΒΊΘ§““Αύ¥”![]() ΒΊ≥ωΖΔ‘»ΥΌ≤Ϋ––ΒΫ
ΒΊ≥ωΖΔ‘»ΥΌ≤Ϋ––ΒΫ![]() ΒΊ.ΝΫΑύΆ§ ±≥ωΖΔΘ§œύœρΕχ––.…η≤Ϋ–– ±ΦδΈΣ
ΒΊ.ΝΫΑύΆ§ ±≥ωΖΔΘ§œύœρΕχ––.…η≤Ϋ–– ±ΦδΈΣ![]() –Γ ±Θ§ΦΉΓΔ““ΝΫΑύάκ
–Γ ±Θ§ΦΉΓΔ““ΝΫΑύάκ![]() ΒΊΒΡΨύάκΖ÷±πΈΣ
ΒΊΒΡΨύάκΖ÷±πΈΣ![]() «ßΟΉΓΔ
«ßΟΉΓΔ![]() «ßΟΉΘ§
«ßΟΉΘ§![]() ΓΔ
ΓΔ![]() ”κ
”κ![]() ΒΡΚ· ΐΙΊœΒΆΦœσ»γΆΦΥυ ΨΘ§ΗυΨίΆΦœσΫβ¥πœ¬Ν–Έ ΧβΘΚ
ΒΡΚ· ΐΙΊœΒΆΦœσ»γΆΦΥυ ΨΘ§ΗυΨίΆΦœσΫβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©÷±Ϋ”–¥≥ω![]() ΓΔ
ΓΔ![]() ”κ
”κ![]() ΒΡΚ· ΐΙΊœΒ ΫΘΜ
ΒΡΚ· ΐΙΊœΒ ΫΘΜ
Θ®2Θ©«σΦΉΓΔ““ΝΫΑύ―ß…ζ≥ωΖΔΚσΘ§ΦΗ–Γ ±œύ”ωΘΩœύ”ω ±““Αύάκ![]() ΒΊΕύ…Ό«ßΟΉΘΩ
ΒΊΕύ…Ό«ßΟΉΘΩ
Θ®3Θ©ΦΉΓΔ““ΝΫΑύœύΨύ4«ßΟΉ ±Υυ”Ο ±Φδ «Εύ…Ό–Γ ±?
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ‘ΎΓςABCΚΆΓςABD÷–Θ§ΓœDABΘΫΓœABCΘΫ90ΓψΘ§ADΘΫABΘΫCBΘ§BDΘΫ6cmΘ§FΈΣœΏΕΈBD…œ“ΜΕ·ΒψΘ§“‘ΟΩΟκ1cmΒΡΥΌΕ»¥”B‘»ΥΌ‘ΥΕ·ΒΫDΘ§ΙΐFΉς÷±œΏFQΓΆAFΘ§«“FQΘΫAFΘ§ΒψQ‘Ύ÷±œΏAFΒΡ”“≤ύΘ§…ηΒψF‘ΥΕ· ±ΦδΈΣtΘ®sΘ©Θ°
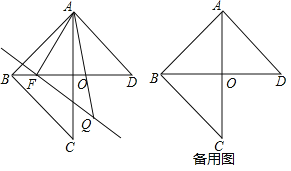
Θ®1Θ©Β±ΓςABFΈΣΒ»―ϋ»ΐΫ«–Έ ±Θ§tΘΫΓΓ ΓΓΘΜ
Θ®2Θ©Β±FΒψ‘ΎœΏΕΈBO…œ ±Θ§ΙΐQΒψΉςQHΓΆBD”ΎΒψHΘ§«σ÷ΛΘΚΓςAOFΓ’ΓςFHQΘΜ
Θ®3Θ©Β±FΒψ‘ΎœΏΕΈOD…œ‘ΥΕ·ΒΡΙΐ≥Χ÷–Θ§ΓςABQΒΡΟφΜΐ «Ζώ±δΜ·ΘΩ»τ≤Μ±δΘ§«σ≥ωΥϋΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
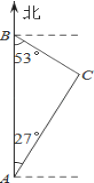
ΓΨΧβΡΩΓΩ»γΆΦΘ§Ϋϊ”φΤΎΦδΘ§Έ“”φ’१‘ΎA¥ΠΖΔœ÷’ΐ±±ΖΫœρB¥Π”–“ΜΥ“Ω…“…¥§÷ΜΘ§≤βΒΟAΓΔBΝΫ¥ΠΨύάκΈΣ99ΚΘάοΘ§Ω…“…¥§÷Μ’ΐ―ΊΡœΤΪΕΪ53ΓψΖΫœρΚΫ––Θ°Έ“”φ’१―ΗΥΌ―Ί±±ΤΪΕΪ27ΓψΖΫœρ«Α»ΞάΙΫΊΘ§2–Γ ±ΚσΗ’ΚΟ‘ΎC¥ΠΫΪΩ…“…¥§÷ΜάΙΫΊΘ°«σΗΟΩ…“…¥§÷ΜΚΫ––ΒΡΥΌΕ»Θ°
Θ®≤ΈΩΦ ΐΨίΘΚsin27ΓψΓ÷![]() Θ§ cos27ΓψΓ÷
Θ§ cos27ΓψΓ÷![]() Θ§ tan27ΓψΓ÷
Θ§ tan27ΓψΓ÷![]() Θ§ sin53ΓψΓ÷
Θ§ sin53ΓψΓ÷![]() Θ§ cos53ΓψΓ÷
Θ§ cos53ΓψΓ÷![]() Θ§ tan53ΓψΓ÷
Θ§ tan53ΓψΓ÷![]() Θ©
Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com