
【题目】如图,AB是⊙O的直径,点E为线段OB上一点(不与O,B重合),作EC⊥OB,交⊙O于点C,作直径CD,过点C的切线交DB的延长线于点P,作AF⊥PC于点F,连接CB.
(1)求证:AC平分∠FAB;
(2)求证:BC2=CECP;
(3)当AB=4![]() 且
且![]() =
=![]() 时,求劣弧
时,求劣弧![]() 的长度.
的长度.

【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】(1)根据已知先证明∠ACF=∠ACE,再根据等角的余角相等即可证得;
(2)只要证明△CBE∽△CPB,可得![]() 即可解决问题;
即可解决问题;
(3)作BM⊥PF于M,则CE=CM=CF,设CE=CM=CF=3a,PC=4a,PM=a,利用相似三角形的性质求出BM,求出tan∠BCM的值即可解决问题;
(1)∵AB是直径,
∴∠ACB=90°,
∴∠BCP+∠ACF=90°,∠ACE+∠BCE=90°,
∵∠BCP=∠BCE,
∴∠ACF=∠ACE,
∵∠AFC=90°,∠AEC=90°,
∴∠FAC=∠EAC,
即AC平分∠FAB;
(2)∵OC=OB,
∴∠OCB=∠OBC,
∵PF是⊙O的切线,CE⊥AB,
∴∠OCP=∠CEB=90°,
∴∠PCB+∠OCB=90°,∠BCE+∠OBC=90°,
∴∠BCE=∠BCP,
∵CD是直径,
∴∠CBD=∠CBP=90°,
∴△CBE∽△CPB,
∴![]() ,
,
∴BC2=CECP;
(3)如图,作BM⊥PF于M.则CE=CM=CF,
设CE=CM=CF=3a,PC=4a,PM=a,
∵∠MCB+∠P=90°,∠P+∠PBM=90°,
∴∠MCB=∠PBM,
∵CD是直径,BM⊥PC,
∴∠CMB=∠BMP=90°,
∴△BMC∽△PMB,
∴![]() ,
,
∴BM2=CMPM=3a2,
∴BM=![]() a,
a,
∴tan∠BCM=![]() ,
,
∴∠BCM=30°,
∴∠OCB=∠OBC=∠BOC=60°,∠BOD=120°,
∴![]() 的长=
的长=![]() .
.



 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径点F、C是半圆弧ABC上的三等份点,连接AC,AF,过点C作CD⊥AF交AF的延长线于点D,垂足为D.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为4,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
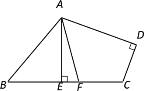
【题目】如图,在四边形ABCD中,∠B=50°,∠C=110°,∠D=90°,AE⊥BC,AF是∠BAD的平分线,与边BC交于点F.求∠EAF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
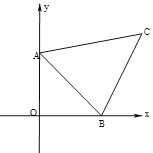
【题目】如图,在平面直角坐标系中,A(0,3),B(3,0),C(5,4),∠OAB=∠OBA=45°,点P为坐标系中第一象限内一点(不与C重合),若△BAP≌△ABC,则点P坐标为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(4,3)是反比例函数y=![]() 在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=
在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=![]() 的图象于点P.
的图象于点P.
(1)求反比例函数y=![]() 的表达式;
的表达式;
(2)求点B的坐标;
(3)求△OAP的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD边长为3,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB延长线于点F,则EF的长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期,大兴区开展了“恰同学少年,品诗词美韵”中华传统诗词大赛活动![]() 小江统计了班级30名同学四月份的诗词背诵数量,具体数据如表所示:
小江统计了班级30名同学四月份的诗词背诵数量,具体数据如表所示:
诗词数量 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
人数 | 3 | 4 | 4 | 5 | 7 | 5 | 1 | 1 |
那么这30名同学四月份诗词背诵数量的众数和中位数分别是![]()
![]()
A. 11,7 B. 7,5 C. 8,8 D. 8,7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作体验
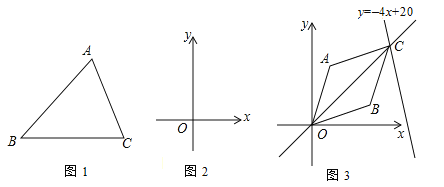
(1)如图1,已知△ABC,请画出△ABC的中线AD,并判断△ABD与△ACD的面积大小关系.
(2)如图2,在平面直角坐标系中,△ABC的边BC在x轴上,已知点A(2,4),B(–1,0),C(3,0),试确定过点A的一条直线l,平分△ABC的面积,请写出直线l的表达式.
综合运用
(3)如图3,在平面直角坐标系中,如果A(1,4),B(3,2),那么在直线y=–4x+20上是否存在一点C,使直线OC恰好平分四边形OACB的面积?若存在,请计算点C的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为促进阳光体育运动发展,计划购进足球、排球充实体育器材,若购买足球30个、排球20个,共需资金2600元,若购买足球40个、排球30个,共需资金3600元.
(1)求足球、排球的价格分别是多少元?
(2)若该校计划购进这两种球的总数是60个,学校至多能够提供资金2800元,求最多能购买足球多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com