
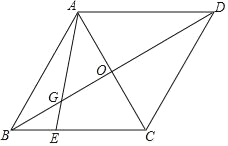
【题目】如图,在菱形ABCD中,点E是BC边上一动点(不与点C重合)对角线AC与BD相交于点O,连接AE,交BD于点G.
(1)根据给出的△AEC,作出它的外接圆⊙F,并标出圆心F(不写作法和证明,保留作图痕迹);
(2)在(1)的条件下,连接EF.①求证:∠AEF=∠DBC;
②记t=GF2+AGGE,当AB=6,BD=6![]() 时,求t的取值范围.
时,求t的取值范围.
【答案】(1)见解析(2)①证明见解析②9≤t≤12
【解析】
(1)作EC的垂直平分线,其与BD的交点即为外心F;
(2)连接AF,EF,利用菱形的性质及外心的定义可证明∠DBC=90°﹣∠ACB及∠AEF=90°﹣∠ACB,可推出结论;
(3)先证△ABG∽△FEG,再证△EFB∽△GFE,由相似三角形的性质可推出t=GF2+AGGE=GF2+GFBG=GF(GF+BG)=GFBF=EF2,在菱形ABCD中,AC⊥BD,EF=AF≥AO,∴EF2≥AO2=32=9,当点F与点O重合时,AF最大,求出此时t的最大值为12,即可写出t的取值范围.
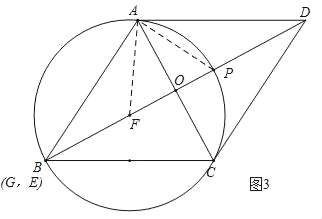
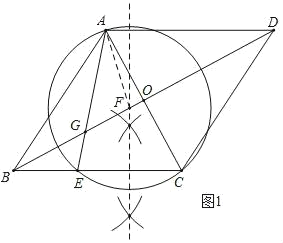
解:(1)如图1,⊙F为所求作的圆;
(2)①证明:
如图2,连接AF,EF,
∵四边形ABCD为菱形,
∴AC⊥BD,
∴∠DBC=90°﹣∠ACB,
∵FA=FE,
∴∠AEF=∠FAE,
∴∠AEF=![]() (180°﹣∠AFE)=90°﹣
(180°﹣∠AFE)=90°﹣![]() ∠AFE,
∠AFE,
又∠ACB=![]() ∠AFE,
∠AFE,
∴∠AEF=90°﹣∠ACB,
又∵∠DBC=90°﹣∠ACB,
∴∠AEF=∠DBC;
②解:∵四边形ABCD为菱形,
∴∠ABD=∠CBD,AO=CO,BO=DO=![]() BD=
BD=![]() ×
×![]() ,
,
在Rt△ABO中,AO=![]() ,
,
又∵∠AGB=∠FGE,∠ABG=∠FEG,
∴△ABG∽△FEG,
![]() ,
,
∴AGGE=GFBG,
∵∠GEF=∠FBE,∠GFE=∠EFB,
∴△EFB∽△GFE,
∴![]() ,
,
∴GFBF=EF2,
∴t=GF2+AGGE=GF2+GFBG=GF(GF+BG)=GFBF=EF2,
在菱形ABCD中,AC⊥BD,EF=AF≥AO,
∴EF2≥AO2=32=9,
如图3,当点F与点O重合时,AF最大,
由题意可知:AF=BF,设AF=x,则OF=3![]()
∵AO2+OF2=AF2,
∴32+(3![]() ﹣x)2=x2,
﹣x)2=x2,
解得,x=2![]() ,
,
∴当x=2![]() 时,t的最大值为12,
时,t的最大值为12,
∴9≤t≤12.



科目:初中数学 来源: 题型:
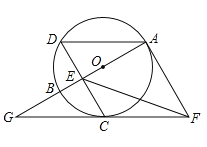
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是圆上一点,弦
是圆上一点,弦![]() 于点
于点![]() ,且
,且![]() .过点
.过点![]() 作
作![]() 的切线,过点
的切线,过点![]() 作
作![]() 的平行线,两直线交于点
的平行线,两直线交于点![]() ,
,![]() 的延长线交
的延长线交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() 与
与![]() 相切;
相切;
(2)连接![]() ,若
,若![]() 的半径为4,求
的半径为4,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】风电已成为我国继煤电、水电之后的第三大电源,风电机组主要由塔杆和叶片组成(如图1),图2是从图1引出的平面图.假设你站在A处测得塔杆顶端C的仰角是55°,沿HA方向水平前进43米到达山底G处,在山顶B处发现正好一叶片到达最高位置,此时测得叶片的顶端D(D、C、H在同一直线上)的仰角是45°.已知叶片的长度为35米(塔杆与叶片连接处的长度忽略不计),山高BG为10米,BG⊥HG,CH⊥AH,求塔杆CH的高.(参考数据:tan55°≈1.4,tan35°≈0.7,sin55°≈0.8,sin35°≈0.6)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程:2(x﹣k)=x﹣4①和关于x的一元二次方程:(k﹣1)x2+2mx+(3﹣k)+n=0②(k、m、n均为实数),方程①的解为非正数.
(1)求k的取值范围;
(2)如果方程②的解为负整数,k﹣m=2,2k﹣n=6且k为整数,求整数m的值;
(3)当方程②有两个实数根x1、x2,满足(x1+x2)(x1﹣x2)+2m(x1﹣x2+m)=n+5,且k为正整数,试判断|m|≤2是否成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
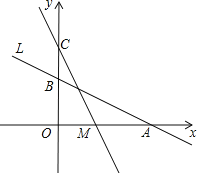
【题目】如图,直线L:y=﹣![]() x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
(1)求A、B两点的坐标;
(2)求△COM的面积S与M的移动时间t之间的函数关系式;
(3)当t为何值时△COM≌△AOB,请直接写出此时t值和M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《中国汉字听写大会》 唤醒了很多人对文字基本功的重视和对汉字文化的学习,某校组织了一次全校2000名学生参加的“汉字听写大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次海选比赛的成绩分布情况,随机抽取了其中200名学生的海选比赛成绩(成绩![]() 取整数,总分100分)作为样本进行整理,得到下列统计图表:
取整数,总分100分)作为样本进行整理,得到下列统计图表:
抽取的200名学生海选成绩分组表
组别 | 海选成绩 |
A组 |
|
B组 |
|
C组 |
|
D组 |
|
E组 |
|

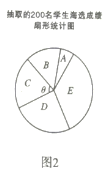
请根据所给信息,解答下列问题
(1)请把图1中的条形统计图补充完整;
(2)在图2的扇形统计图中,表示![]() 组扇形的圆心角
组扇形的圆心角![]() 的度数为_______度;
的度数为_______度;
(3)规定海选成绩在90分以上(包括90分)记为“优等”,请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人;
(4)经过统计发现,在![]() 组中,有2位男生和2位女生获得了满分,如果从这4人中挑选2人代表学校参加比赛,请用树状图或列表法求出所选两人正好是一男一女的概率是多少?
组中,有2位男生和2位女生获得了满分,如果从这4人中挑选2人代表学校参加比赛,请用树状图或列表法求出所选两人正好是一男一女的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学共有3个一样规模的大餐厅和2个一样规模的小餐厅,经过测试同时开放2个大餐厅和1个小餐厅,可供3000名学生就餐;同时开放1个大餐厅,1个小餐厅,可供1700名学生就餐.
(1)请问1个大餐厅、1个小餐厅分别可供多少名学生就餐.
(2)如果3个大餐厅和2个小餐厅全部开放,那么能否供全校4500名学生就餐?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形![]() 中,
中,![]() 分别为边
分别为边![]() ,
,![]() ,
,![]() ,
,![]() 上的点(不与端点重合).对于任意菱形
上的点(不与端点重合).对于任意菱形![]() ,下面四个结论中:①存在无数个四边形
,下面四个结论中:①存在无数个四边形![]() 是平行四边形;②存在无数个四边形
是平行四边形;②存在无数个四边形![]() 是菱形;③存在无数个四边形
是菱形;③存在无数个四边形![]() 是矩形;④存在无数个四边形
是矩形;④存在无数个四边形![]() 是正方形;所有正确结论的序号是______.
是正方形;所有正确结论的序号是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com