
【题目】在△ABC中,AC=BC,∠ACB=90°,CE是过C点的一条直线,AD⊥CE于D,BE⊥CE于E,DE=4cm,AD=2cm,则BE=( )
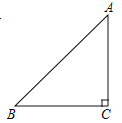
A. 2cm B. 4cm C. 6cm或2cm D. 6cm
【答案】C
【解析】试题解析:分为两种情况:
①如图1,当CE在△ABC内.
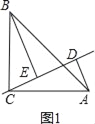
∵AD⊥CE,∠BCA=90°,
∴∠ADC=∠BCA=90°,
∴∠DCA+∠BCE=90°,∠DCA+∠DAC=90°,
∴∠DAC=∠BCE,
∵AD⊥CE,BE⊥CE,
∴∠ADC=∠BEC=90°,
在△ACD和△CBE中,
 ,
,
∴△ACD≌△CBE(AAS)
∴CE=AD=2cm,CD=BE,
BE=CD=CE+DE=2cm+4cm=6cm;
②如图2,当CE在△ABC外.

∵在△EBC和△DAC中,
 ,
,
∴△ACD≌△CBE(AAS),
∴CE=AD=2cm,BE=CD,
∴BE=CD=DE﹣AD=4cm﹣2cm=2cm,
故答案为:6或2.
故选C.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
【题目】某小组做“用频率估计概率”的试验时,统计了某一结果出现的频率,绘制了如图所示的折线统计图,则符合这一结果的试验最有可能的是( )

A. 在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B. 一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
C. 暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球
D. 掷一个质地均匀的正六面体骰子,向上的面点数是4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某小区内有一块长、宽比为2∶1的矩形空地,计划在该空地上修筑两条宽均为2 m的互相垂直的小路,余下的四块小矩形空地铺成草坪,如果四块草坪的面积之和为312 m2,请求出原来大矩形空地的长和宽.
(1)请找出上述问题中的等量关系:_________________;
(2)若设大矩形空地的宽为xm,可列出的方程为_____________,方程的解为__________,原来大矩形空地的长和宽分别为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O(0,0),B(0,1)是正方形OBB1C的两个顶点,以它的对角线OB1为一边作正方形OB1B2C1 ,以正方形OB1B2C1的对角线OB2为一边作正方形OB2B3C2 ,再以正方形OB2B3C2的对角线OB3为一边作正方形OB3B4C3 ,…,依次进行下去,则点B6的坐标是( )

A. (﹣8,0) B. (0,﹣8) C. (![]() ,0) D. (
,0) D. (![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
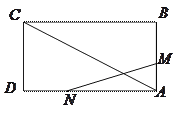
【题目】如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s的速度向![]() 点匀速运动;同时,动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动,问:是否存在时刻
点匀速运动;同时,动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动,问:是否存在时刻![]() ,使以A,M,N为顶点的三角形与△ACD相似?若存在,求
,使以A,M,N为顶点的三角形与△ACD相似?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
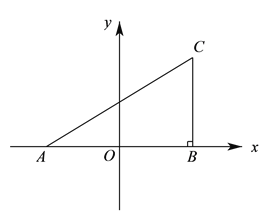
【题目】如图①,在平面直角坐标系中, ![]() ,
, ![]() ,且满足
,且满足![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() .
.
(![]() )求
)求![]() 的面积.
的面积.
(![]() )在
)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 和
和![]() 的面积相等?若存在,求出
的面积相等?若存在,求出![]() 点坐标;若不存在,说明理由.
点坐标;若不存在,说明理由.
(![]() )动点
)动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 的速度沿射线
的速度沿射线![]() 运动,如果在运动过程中
运动,如果在运动过程中![]() 为等腰三角形,求出点
为等腰三角形,求出点![]() 运动的时间.
运动的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD的各边与坐标轴都平行,点A,C的坐标分别为(-1,1),(![]() ,-2
,-2![]() ).
).
(1)求点B,D的坐标.
(2)一动点P从点A出发,沿长方形的边AB,BC运动至点C停止,运动速度为每秒![]() 个单位长度,设运动时间为t s.
个单位长度,设运动时间为t s.
①当t=1时,求点P的坐标;
②当t=3时,求三角形PDC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
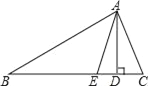
【题目】已知,如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠ABC=30°,∠ACB=50°.
(1)求∠DAE的度数;
(2)写出∠DAE与∠ACB﹣∠ABC的数量关系: ,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
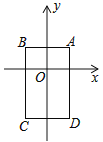
【题目】如图,在平面直角坐标系中,已知点A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),把一根长为2017个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是( )
A. (﹣1,﹣2) B. (―1,1)
C. (-1,-1) D. (1,―2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com