
 ��ͼ����A��B���߶�MN���������ϣ���A��M��N��B��Ӧ�����ֱַ�Ϊ-1��0��2��11���߶�MN���������������ÿ��1����λ���ٶ��ƶ����ƶ�ʱ��Ϊt�룮
��ͼ����A��B���߶�MN���������ϣ���A��M��N��B��Ӧ�����ֱַ�Ϊ-1��0��2��11���߶�MN���������������ÿ��1����λ���ٶ��ƶ����ƶ�ʱ��Ϊt�룮���� ��1�����ݵ�M��ʼ��ʾ����������˶��ٶȺ�ʱ�䣬���ɵó��˶����M�ı�ʾ�����������ݵ�A��ʾ����Ϊ-1���ɵó����ۣ�
��2���ֱ��ҳ�AM��BN������AM+BN=11�����г�����t�ĺ�����ֵ���ŵ�һԪһ�η��̣��ⷽ�̼��ɵó����ۣ�
��3�������ܹ���ȣ��ҳ�AM��BN������AM=BN�����г�����t�ĺ�����ֵ���ŵ�һԪһ�η��̣��ⷽ�̼��ɵó����ۣ�
��� �⣺��1���ߵ�A��M��N��Ӧ�����ֱַ�Ϊ-1��0��2���߶�MN���������������ÿ��1����λ���ٶ��ƶ����ƶ�ʱ��Ϊt�룬
���ƶ���M��ʾ����Ϊt��N��ʾ����Ϊt+2��
��AM=t-��-1��=t+1��
�ʴ�Ϊ��t+1��
��2���ɣ�1����֪��BN=|11-��t+2��|=|9-t|��
��AM+BN=11��
��t+1+|9-t|=11��
��ã�t=$\frac{19}{2}$��
�ʴ�Ϊ��$\frac{19}{2}$��
��3����������ȣ����A��ʾ����Ϊ2t-1��M��ʾ����Ϊt��N��ʾ����Ϊt+2��B��ʾ����Ϊ11-t��
��AM=|2t-1-t|=|t-1|��BN=|t+2-��11-t��|=|2t-9|��
��AM=BN��
��|t-1|=|2t-9|��
��ã�t1=$\frac{10}{3}$��t2=8��
�����˶��Ĺ�����AM��BN����ȣ���ʱ�˶���ʱ��Ϊ$\frac{10}{3}$���8�룮
���� ���⿼���������Լ�һԪһ�η��̵�Ӧ�ã�����������ϵ�г�һԪһ�η����ǽ���Ĺؼ���


 �ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
�ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=��x-3��2-1 | B�� | y=��x+1��2+5 | C�� | y=��x+1��2-1 | D�� | y=��x-3��2+5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
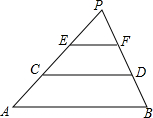 ��ͼ����֪AB��CD��EF��AC=CE=EP����PEF�������2�����ı���ABCD������ǣ�������
��ͼ����֪AB��CD��EF��AC=CE=EP����PEF�������2�����ı���ABCD������ǣ�������| A�� | 18 | B�� | 16 | C�� | 12 | D�� | 10 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com