
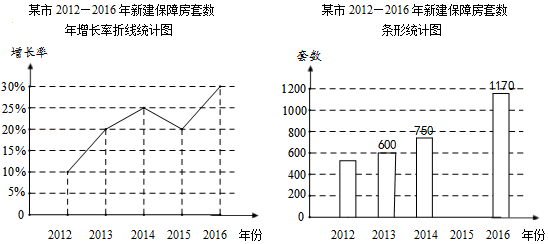
分析 (1)根据2015年新建保障房的增长率比2014年的增长率减少,并不是建设住房减少,即可得出答案;
(2)根据住房建设增长率求出2012年和2015年建设住房的套数,即可得出答案;
(3)根据(2)中所求求出平均数即可.
解答 解:(1)该市2015年新建保障房的增长率比2014年的增长率减少了,
但是保障房的总数在增加,故小丽的说法错误;
(2)2015年保障房的套数为:750×(1+20%)=900(套),
设2012年保障房的套数为x套,则有:x(1+20%)=600,则x=500,
如图: ;
;
(3)这5年平均每年新建保障房的套数为:(500+600+750+900+1170)÷5=784(套),
答:这5年平均每年新建保障房的套数为784套.
点评 本题主要考查了条形图与折线图的综合应用,正确由两图得出正确信息是解题关键.


科目:初中数学 来源: 题型:解答题
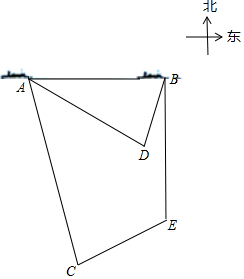 如图,我国某艘海舰船沿正东方向由A向B例行巡航南海部分区域,在航线AB同一水平面上,有三座岛屿C、D、E.船在A处时,测得岛C在A处南偏东15°方向距离A处$\sqrt{2}$a(a>0)海里,岛D在A处南偏东60°方向距离A处a海里,岛E在A处东南方向,当船航行到达B处时,此时测得岛E恰好在船的正南方.
如图,我国某艘海舰船沿正东方向由A向B例行巡航南海部分区域,在航线AB同一水平面上,有三座岛屿C、D、E.船在A处时,测得岛C在A处南偏东15°方向距离A处$\sqrt{2}$a(a>0)海里,岛D在A处南偏东60°方向距离A处a海里,岛E在A处东南方向,当船航行到达B处时,此时测得岛E恰好在船的正南方.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
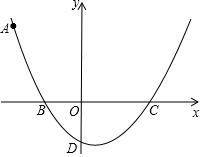 如图,在平面直角坐标系内,点O为坐标原点,经过点A(-4,4)的抛物线y=$\frac{1}{k}$(x+2)(x+a)交x轴负半轴于点B,交x轴正半轴于点C,交y轴于点D(0,-2).
如图,在平面直角坐标系内,点O为坐标原点,经过点A(-4,4)的抛物线y=$\frac{1}{k}$(x+2)(x+a)交x轴负半轴于点B,交x轴正半轴于点C,交y轴于点D(0,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某教学楼AB的后面有一建筑物CD,当光线与地面夹角是22°时,教学楼在建筑物的墙上留下高2米的影子CE;而当光线与地面夹角是45°时,教学楼顶A在地面上的影子F与墙角C有13米的距离(B、F、C在一条直线上),求教学楼AB的高度(sin22°≈$\frac{3}{8}$,cos22°≈$\frac{15}{16}$,tan22°≈$\frac{2}{5}$)
如图,某教学楼AB的后面有一建筑物CD,当光线与地面夹角是22°时,教学楼在建筑物的墙上留下高2米的影子CE;而当光线与地面夹角是45°时,教学楼顶A在地面上的影子F与墙角C有13米的距离(B、F、C在一条直线上),求教学楼AB的高度(sin22°≈$\frac{3}{8}$,cos22°≈$\frac{15}{16}$,tan22°≈$\frac{2}{5}$)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com