练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．已知一个矩形的宽是长的一半，对角线长为3$\sqrt{5}$，则该矩形的面积为18．

    分析 设矩形的宽AB=x，则BC=2x，由勾股定理得出方程，解方程求出AB、BC，矩形ABCD的面积=AB•BC，即可得出结果．

    解答 解：如图所示：
    ∵四边形ABCD是矩形，
    ∴∠ABC=90°，AB=CD，AD=BC，
    设矩形的宽AB=x，则BC=2x，
    由勾股定理得：AB2+BC2=AC2，
    即x2+（2x）2=（3$\sqrt{5}$）2，
    解得：x=3，
    ∴2x=6，
    ∴AB=3，BC=6，
    ∴矩形ABCD的面积=AB•BC=3×6=18；
    故答案为：18．

    点评 本题考查了矩形的性质、勾股定理、矩形面积的计算方法；熟练掌握矩形的性质，并能进行推理计算是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    13．如图，矩形ABCD中，AB=6cm，BC=8cm，点P在AD边上移动（不与点A、D重合），过点C作BP的垂线，垂足为点Q．设BP的长为xcm，CQ的长为ycm，求y与x之间的函数关系式及自变量x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．设A、B、C、D、E都是整数，且有|A-B|=19，|B-C|=7，|C-D|=5，|D-E|=4，|E-A|=11，又A+B+C+D+E=56，求E．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．小王解方程x（2x+3）-6（2x+3）=0，小王的解法是这样的：移项，得x（2x+3）=6（2x+3），方程两边都除以（2x+3），得x=6，小王所：“我的方法多简便”．可老师却说他做错了，请你指出他错误的原因，并求出正确的答案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．已知一个两位数等于其中个位上数字的平方，且个位数字比十位数字大3，求这个两位数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

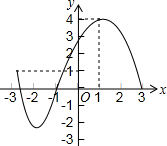    7．已知某一函数的图象如图所示，根据图象回答下列问题：
    （1）确定自变量x的取值范围；
    （2）求当x=0，x=-3时y的值；
    （3）求当y=3时，x的值；
    （4）当x取何值时，函数值y最大？
    （5）当x在什么范围内，y随x的增大而增大？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．如图所示，一架云梯AB斜靠在一面墙上，设木棍的中点为P．若木棍A端沿墙下滑，且B端沿底面向右滑行．
    （1）请判断木棍滑动的过程中，点P到点O的距离是否变化，并简述理由；
    （2）若梯子底端B离墙7米，如果梯子的顶端A下滑4米至A′处，那么梯子的底部在水平方向滑动8米至B′处，求梯子的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

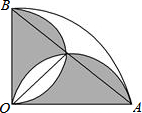    11．半径1cm，圆心角90度的扇形OAB中，分别以OA，OB为直径作半圆，则阴影部分（两个半圆除了重叠部分其余部分）面积为$\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

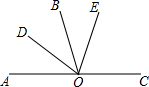    12．已知，O是直线AC上一点，OD平分∠AOB，∠BOE=$\frac{1}{2}$∠EOC，∠DOE=72°，OB是∠DOE的平分线吗？说明理由．

    查看答案和解析>>

    同步练习册答案