
【题目】如图在平面直角坐标系中,四边形OABC是正方形,点A的坐标是(4,0),点p为边AB上的一点,![]() CPB=60°,沿CP折叠正方形后,点B落在平面内B’处,B’的坐标为( )
CPB=60°,沿CP折叠正方形后,点B落在平面内B’处,B’的坐标为( )
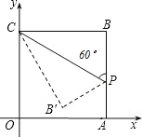
A.(2, 2![]() )B.(
)B.(![]() , 2-2
, 2-2![]() )C.(2, 4-2
)C.(2, 4-2![]() )D.(
)D.(![]() , 4-2
, 4-2![]() )
)
【答案】C
【解析】
作B′E⊥y轴于E,B′F⊥x轴于F,根据正方形的性质OC=BC=4,∠B=90°,由∠BPC=60°得∠1=30°,再根据折叠的性质得到∠1=∠2=30°,CB′=CB=4,所以∠3=30°,在Rt△CB′E中,根据含30度的直角三角形三边的关系得到B′E=![]() CB′=2,CE=
CB′=2,CE=![]() B′E=2
B′E=2![]() ,则OE=4-2
,则OE=4-2![]() ,所以B′F=4-2
,所以B′F=4-2![]() ,然后可写出B′点坐标.
,然后可写出B′点坐标.
解:作B′E⊥y轴于E,B′F⊥x轴于F,如图,
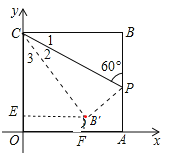
∵四边形OABC是正方形,点A的坐标是(4,0),
∴OC=BC=4,∠B=90°,
∵∠BPC=60°,
∴∠1=30°,
∵△CPB沿CP折叠,使得点B落在B′处,
∴∠1=∠2=30°,CB′=CB=4,
∴∠3=30°,
在Rt△CB′E中,B′E=![]() CB′=2,CE=
CB′=2,CE=![]() =2
=2![]() ,
,
∴OE=OC-CE=4-2![]() ,
,
∴B′F=OE=4-2![]() ,
,
∴B′点坐标为(2,4-2![]() ).
).
故选:C.


科目:初中数学 来源: 题型:
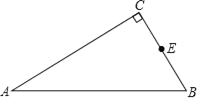
【题目】已知,如图,△ABC中,∠C=90°,E为BC边中点.
(1)尺规作图:以AC为直径,作⊙O,交AB于点D(保留作图痕迹,不需写作法).
(2)连结DE,求证:DE为⊙O的切线;
(3)若AC=5,DE=![]() ,求BD的长.
,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C = 90°,点O是斜边AB上一定点,到点O的距离等于OB的所有点组成图形W,图形W与AB,BC分别交于点D,E,连接AE,DE,∠AED=∠B.

(1)判断图形W与AE所在直线的公共点个数,并证明.
(2)若![]() ,
,![]() ,求OB.
,求OB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知小正方形ABCD的面积为1,把它的各边延长一倍得到新正方形A1B1C1D1;把正方形A1B1C1D1边长按原法延长一倍得到正方形A2B2C2D2(如图(2));正方形A2B2C2D2的面积为________,以此下去…,则正方形AnBnCnDn的面积为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提升干线公路美化度,相关部门拟定派一个工程队对39000米的公路进行路面“白改黑”工程.该工程队计划使用一大一小两种型号设备交替的方式施工,原计划小型设备每小时铺设路面30米,大型设备每小时铺设路面60米
(1)由于小型设备工作效率较低,该工程队计划使用大型设备的时间比使用小型设备的时间多![]() ,当这个工程完工时,小型设备的使用时间至少为多少小时?
,当这个工程完工时,小型设备的使用时间至少为多少小时?
(2)通过勘察、又新增了部分支线公路美化,结果此工程的实际施工里程比最初拟定的最少里程39000米多了9000米,于是在实际施工中,小型设备在铺设公路效率不变的情况下,使用时间比(1)中的最小值多![]() ,同时,因为工人操作大型设备不够熟练,使得大型设备铺设公路的效率比原计划下降了
,同时,因为工人操作大型设备不够熟练,使得大型设备铺设公路的效率比原计划下降了![]() ,使用时间比(1)中大型设备使用的最短时间多
,使用时间比(1)中大型设备使用的最短时间多![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,将
,将![]() 绕点
绕点![]() 按逆时针方向旋转,得到
按逆时针方向旋转,得到![]() .
.
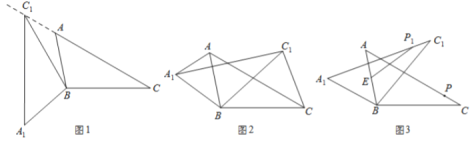
(1)如图 1,当点![]() 在线段
在线段![]() 的延长线上时,求
的延长线上时,求![]() 的度数;
的度数;
(2)如图 2,连接![]() ,
,![]() .若
.若![]() 的面积为 3,求
的面积为 3,求![]() 的面积;
的面积;
(3)如图 3,点![]() 为线段
为线段![]() 中点,点
中点,点![]() 是线段
是线段![]() 上的动点,在
上的动点,在![]() 绕点
绕点![]() 按逆时针方向旋转的过程中,点
按逆时针方向旋转的过程中,点![]() 的对应点是点
的对应点是点![]() ,求线段
,求线段![]() 长度的最大值与最小值.
长度的最大值与最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从相距420km的A、B两地相向而行,乙车比甲车先出发1小时,两车分别以各自的速度匀速行驶,途经C地(A、B、C三地在同一条直线上).甲车到达C地后因有事立即按原路原速返回A地,乙车从B地直达A地,甲、乙两车距各自出发地的路程y(千米)与甲车行驶所用的时间x(小时)的关系如图所示,结合图象信息回答下列问题:
(1)甲车的速度是 千米/时,乙车的速度是 千米/时;
(2)求甲车距它出发地的路程y(千米)与它行驶所用的时间x(小时)之间的函数关系式;
(3)甲车出发多长时间后两车相距90千米?请你直接写出答案.

查看答案和解析>>
科目:初中数学 来源: 题型:
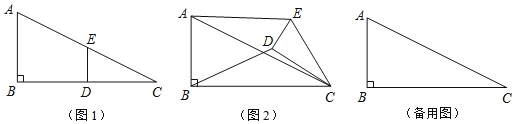
【题目】如图1,在![]() 中,∠B=90°,
中,∠B=90°,![]() ,点D,E分别是边BC,AC的中点,连接
,点D,E分别是边BC,AC的中点,连接![]() 将
将![]() 绕点C按顺时针方向旋转,记旋转角为
绕点C按顺时针方向旋转,记旋转角为![]() .
.
![]() 问题发现:
问题发现:
![]() 当
当![]() 时,
时,![]() _____;
_____;![]() 当
当![]() 时,
时,![]() _____.
_____.
![]() 拓展探究:
拓展探究:
试判断:当![]() 时,
时,![]() 的大小有无变化?请仅就图2的情况给出证明.
的大小有无变化?请仅就图2的情况给出证明.
![]() 问题解决:
问题解决:
当![]() 旋转至A、D、E三点共线时,直接写出线段BD的长.
旋转至A、D、E三点共线时,直接写出线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
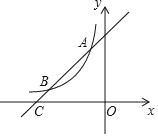
【题目】如图,一次函数y=x+4的图象与反比例函数y=![]() (k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求a,k的值及点B的坐标;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,直接写出点P的坐标.
S△BOC,直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com