
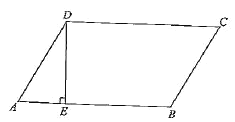
【题目】如图,在平行四边形![]() 中,
中,![]() ,
, ![]() ,
,![]() ,
,![]() , 垂足为
, 垂足为![]() ,在平行四边形的边上有一点
,在平行四边形的边上有一点![]() ,且
,且![]() .将平行四边形折叠,使点
.将平行四边形折叠,使点![]() 与点
与点![]() 合,折痕所在直线与平行四边形交于点
合,折痕所在直线与平行四边形交于点![]() 、
、![]() .
.
(1)求![]() 的长;
的长;
(2)请补全图形并求折痕![]() 的长.
的长.
【答案】(1)![]() ;(2)补全图形见解析;折痕
;(2)补全图形见解析;折痕![]() 的长为5或
的长为5或![]() .
.
【解析】
(1)在Rt△ADE中,![]() ,
,![]() ,求得
,求得![]() ,再根据勾股定理即可求解;
,再根据勾股定理即可求解;
(2)分点O在AB和AD两类讨论,当点![]() 在
在![]() 上时,可得
上时,可得![]() 是等边三角形.求得
是等边三角形.求得![]() ;点点O在AD上时,过点
;点点O在AD上时,过点![]() 、
、![]() 分别作
分别作![]() ,
, ![]() ,
,
垂足分别为![]() 、
、![]() , 连接
, 连接![]() ,
,![]() .求出
.求出![]() ,
,![]() ,
,![]() ,
,![]() 根据折叠性质,结合勾股定理,求出
根据折叠性质,结合勾股定理,求出![]() ,进而求出
,进而求出![]() ,利用面积法即可求得
,利用面积法即可求得![]() .
.
(1)∵![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
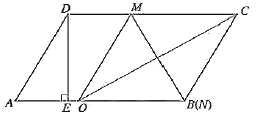
(2)如图1所示,当点![]() 在
在![]() 上时,
上时,
∵![]() ,
, ![]() ,
,
∴![]() .
.
∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,![]() ,
,![]() .
.
∴![]() .
.
∵将平行四边形折叠,使点![]() 与点
与点![]() 重合,
重合,
∴折痕![]() 垂直平分
垂直平分![]() ,即
,即![]() ,
,
![]() .
.
∵折痕![]() 与平行四边形
与平行四边形![]() 的边
的边![]() 交于点
交于点![]() ,
,
∴点![]() 与点
与点![]() 重合.
重合.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() 是等边三角形.
是等边三角形.
∴![]() .
.
如图2所示,当点![]() 在
在![]() 上时,
上时,

过点![]() 、
、![]() 分别作
分别作![]() ,
, ![]() ,
,
垂足分别为![]() 、
、![]() , 连接
, 连接![]() ,
,![]() .
.
∵四边形![]() 是平行四边形,
是平行四边形,![]() ,
,
∴![]() ,
,![]() ,
,![]()
∴![]() ,
,![]()
∵![]() ,
, ![]() ,
,
∴![]() .
.
∵在![]() 中,
中,![]() ,
,
∴![]() .
.
∴![]() ,
,
![]() .
.
∴在![]() 中,
中,![]() ,
,
由折叠可知,![]() ,
,![]() .
.
∴在![]() 中,
中,![]() ,
,
即![]() .
.
∴![]() .
.
∴![]() ,
,![]() ,
,
∴![]() .
.
∴四边形![]() 为矩形.
为矩形.
∴![]() ,
,
∵![]() ,
,
∴![]()
∴![]() .
.
综上所述,折痕![]() 的长为5或
的长为5或![]() .
.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:初中数学 来源: 题型:
【题目】如图,点A,B,C在⊙O上,∠ABC=29°,过点C作⊙O的切线交OA的延长线于点D,则∠D的大小为( )
A.29°
B.32°
C.42°
D.58°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,自来水厂A和村庄B在小河l的两侧,现要在A,B间铺设一条输水管道.为了搞好工程预算,需测算出A,B间的距离.一小船在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q处,测得A位于北偏西49°方向,B位于南偏西41°方向.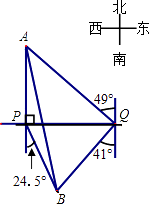
(1)线段BQ与PQ是否相等?请说明理由;
(2)求A,B间的距离.(参考数据cos41°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
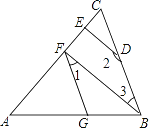
【题目】如图,∠AGF=∠ABC,∠1+∠2=180°.
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=150°,求∠AFG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题: 如图1,在矩形![]() 中,对角线
中,对角线![]() 、
、![]() 相交于点
相交于点![]() ,且
,且![]() ,点
,点![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的中点,连接所
的中点,连接所![]() 、
、![]() 、
、![]() .
.
求证:![]() 是等边三角形.
是等边三角形.
小明经探究发现,连接![]() 、
、![]() (如图2),从而可证
(如图2),从而可证![]() ,
, ![]() ,使问题得到解决.
,使问题得到解决.

(1)请你按照小明的探究思路,完成他的证明过程;
参考小明思考问题的方法或用其他的方法,解决下面的问题:
(2)如图3,在四边形![]() 中,
中, ![]() ,
,![]() , 对角线
, 对角线![]() 、
、![]() 相交于点
相交于点![]() ,且
,且![]() (
(![]() ),点
),点![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的中点,连接
的中点,连接![]() 、
、![]() 、
、![]() .
.
①否存在与![]() 相等的线段?若存在,请找出并证明;若不存在,说明理由.
相等的线段?若存在,请找出并证明;若不存在,说明理由.
②求![]() 的度数.(用含
的度数.(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系,O为坐标原点,点A(﹣1,0),点B(0, ![]() ).
).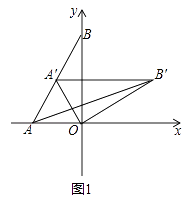
(1)求∠BAO的度数;
(2)如图1,将△AOB绕点O顺时针得△A′OB′,当A′恰好落在AB边上时,设△AB′O的面积为S1 , △BA′O的面积为S2 , S1与S2有何关系?为什么?
(3)若将△AOB绕点O顺时针旋转到如图2所示的位置,S1与S2的关系发生变化了吗?证明你的判断.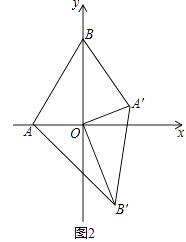
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设![]() ,
, ![]() ,……,
,……, ![]() ,(n为正整数)
,(n为正整数)
(1)试说明![]() 是8的倍数;
是8的倍数;
(2)若△ABC的三条边长分别为![]() 、
、![]() 、
、![]() (
(![]() 为正整数)
为正整数)
①求![]() 的取值范围.
的取值范围.
②是否存在这样的![]() ,使得△ABC的周长为一个完全平方数,若存在,试举出一例,若不存在,说明理由.
,使得△ABC的周长为一个完全平方数,若存在,试举出一例,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P在⊙O的直径BA延长线上,PC与⊙O相切,切点为C,点D在⊙O上,连接PD、BD,已知PC=PD=BC.下列结论:
①PD与⊙O相切;
②四边形PCBD是菱形;
③PO=AB;
④∠PDB=120°.
其中,正确的个数是( )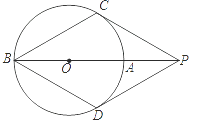
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com