练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在ABCD中，点E是AD边上一点，AE：ED＝1：2，连接AC、BE交于点F.若S△AEF＝1，则S四边形CDEF＝_______.

    【答案】11

    【解析】

    先根据平行四边形的性质易得，根据相似三角形的判定可得△AFE∽△CFB，再根据相似三角形的性质得到△BFC的面积，，进而得到△AFB的面积，即可得△ABC的面积，再根据平行四边形的性质即可得解.

    解：∵AE：ED＝1：2，

    ∴AE：AD＝1：3，

    ∵AD=BC，

    ∴AE：BC＝1：3，

    ∵AD∥BC，

    ∴△AFE∽△CFB，

    ∴，

    ∴，

    ∴S△BCF=9，

    ∵，

    ∴S△AFB=3，

    ∴S△ACD =S△ABC = S△BCF+S△AFB=12，

    ∴S四边形CDEF＝S△ACD﹣S△AEF＝12﹣1=11.

    故答案为：11.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某村启动“脱贫攻坚”项目，根据当地的地理条件，要在一座高为1000m的上种植一种经济作物．农业技术人员在种植前进行了主要相关因素的调查统计，结果如下：

    ①这座山的山脚下温度约为22°C，山高h（单位：m）每增加100m，温度T（单位：°C）下降约0.5°C；

    ②该作物的种植成活率p受温度T影响，且在19°C时达到最大．大致如表：

    温度T°C

    21

    20.5

    20

    19.5

    19

    18.5

    18

    17.5

    种植成活率p

    90%

    92%

    94%

    96%

    98%

    96%

    94%

    92%

    ③该作物在这座山上的种植量w受山高h影响，大致如图1：

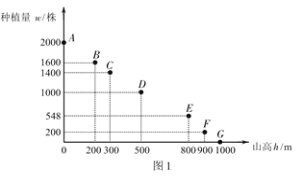
    （1）求T关于h的函数解析式，并求T的最小值；

    （2）若要求该作物种植成活率p不低于92%，根据上述统计结果，山高h为多少米时该作物的成活量最大？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

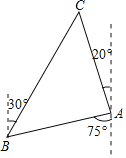
    【题目】如图，一艘渔船位于灯塔A的南偏西75°方向的B处，距离A处30海里，渔船沿北偏东30°方向追寻鱼群，航行一段时间后，到达位于A处北偏西20°方向的C处，渔船出现了故障立即向正在灯塔A处的巡逻船发出求救信号．巡逻船收到信号后以40海里每小时的速度前往救助，请问巡逻船多少分钟能够到达C处？（参考数据：≈1.4，sin40°≈0.64，cos40°≈0.77，tan40°≈0.84，最后结果精确到1分钟）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

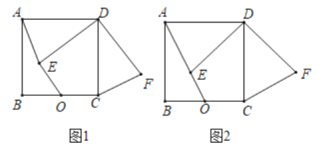
    【题目】已知正方形ABCD的对角线AC，BD相交于点O．

    （1）如图1，E，G分别是OB，OC上的点，CE与DG的延长线相交于点F．若DF⊥CE，求证：OE＝OG；

    （2）如图2，H是BC上的点，过点H作EH⊥BC，交线段OB于点E，连结DH交CE于点F，交OC于点G．若OE＝OG，

    ①求证：∠ODG＝∠OCE；

    ②当AB＝1时，求HC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：有一组邻边相等，并且它们的夹角是直角的凸四边形叫做等腰直角四边形．

    （1）如图1，等腰直角四边形ABCD，AB=BC，∠ABC=90°．

    ①若AB=CD=1，AB∥CD，求对角线BD的长．

    ②若AC⊥BD，求证：AD=CD；

    （2）如图2，在矩形ABCD中，AB=5，BC=9，点P是对角线BD上一点，且BP=2PD，过点P作直线分别交边AD，BC于点E，F，使四边形ABFE是等腰直角四边形，求AE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

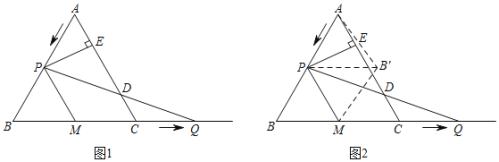
    【题目】如图1，在等边△ABC中，AB＝6cm，动点P从点A出发以1cm/s的速度沿AB匀速运动，动点Q同时从点C出发以同样的速度沿BC的延长线方向匀速运动，当点P到达点B时，点P、Q同时停止运动．设运动时间为t（s），过点P作PE⊥AC于E，PQ交AC边于D，线段BC的中点为M，连接PM．

    （1）当t为何值时，△CDQ与△MPQ相似；

    （2）在点P、Q运动过程中，点D、E也随之运动，线段DE的长度是否会发生变化？若发生变化，请说明理由，若不发生变化，求DE的长；

    （3）如图2，将△BPM沿直线PM翻折，得△B'PM，连接AB'，当t为何值时，AB'的值最小？并求出最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】昆明市某中学“综合实践活动”棋类社团前两次购买的两种材质的围棋采购如表（近期两种材质的围棋的售价一直不变）：

    塑料围棋

    玻璃围棋

    总价（元）

    第一次（盒）

    第二次（盒）

    （1）若该社团计划再采购这两种材质的围棋各盒，则需要多少元；

    （2）若该社团准备购买这两种材质的围棋共盒，且要求塑料围棋的数量不多于玻璃围棋数量的倍，请设计出最省钱的购买方案，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

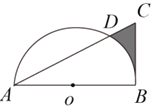
    【题目】如图，在Rt△ABC中，∠ABC=90°，AB=，BC=2，以AB的中点为圆心，OA的长为半径作半圆交AC于点D，则图中阴影部分的面积为( )

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形中，，是边的中点，点是正方形内一动点，，连接，将线段绕点逆时针旋转得，连接，．

    （1）如图1，求证：；

    （2）如图2，若，，三点共线，求点到直线的距离．

    查看答案和解析>>

    同步练习册答案