
ЁОЬтФПЁПФГХЉПЦЫљдкЯрЭЌЬѕМўЯТзіФГзїЮяжжзгЗЂбПТЪЕФЪЕбщЃЌНсЙћШчБэЫљЪОЃК
жжзгИіЪ§ | 200 | 300 | 500 | 700 | 800 | 900 | 1000 |
ЗЂбПжжзгИіЪ§ | 187 | 282 | 435 | 624 | 718 | 814 | 901 |
ЗЂбПжжзгЦЕТЪ | 0.935 | 0.940 | 0.870 | 0.891 | 0.898 | 0.904 | 0.901 |
ЯТУцгаЫФИіЭЦЖЯЃКЂйжжзгИіЪ§ЪЧ700ЪБЃЌЗЂбПжжзгЕФИіЪ§ЪЧ624ЃЎЫљвджжзгЗЂбПЕФИХТЪЪЧ0.891ЃЛЂкЫцзХВЮМгЪЕбщЕФжжзгЪ§СПЕФдіМгЃЌЗЂбПжжзгЕФЦЕТЪдк0.9ИННќАкЖЏЃЌЯдЪОГівЛЖЈЕФЮШЖЈадЃЎПЩвдЙРМЦжжзгЗЂбПЕФИХТЪдМЮЊ0.9(ОЋШЗЕН0.1)ЃЛЂлЪЕбщЕФжжзгИіЪ§зюЖрЕФФЧДЮЪЕбщЕУЕНЕФЗЂбПжжзгЕФЦЕТЪвЛЖЈЪЧжжзгЗЂбПЕФИХТЪЃЛЂмШєгУЦЕТЪЙРМЦжжзгЗЂбПЕФИХТЪдМЮЊ0.9ЃЌдђПЩвдЙРМЦ![]() жжзгДѓдМга
жжзгДѓдМга![]() ЕФжжзгВЛФмЗЂбПЃЎЦфжаКЯРэЕФЪЧ( )
ЕФжжзгВЛФмЗЂбПЃЎЦфжаКЯРэЕФЪЧ( )
A.ЂйЂкB.ЂлЂмC.ЂкЂлD.ЂкЂм
ЁОД№АИЁПD
ЁОНтЮіЁП
ИљОнФГХЉПЦЫљдкЯрЭЌЬѕМўЯТзіФГзїЮяжжзгЗЂбПТЪЕФЪдбщБэЃЌПЩЕУДѓСПжиИДЪдбщЗЂбПТЪж№НЅЮШЖЈдк0.9зѓгвЃЌгкЪЧЕУЕНжжзгЗЂбПЕФИХТЪдМЮЊ0.9ЃЌОнДЫЧѓГі![]() жжзгжаДѓдМга
жжзгжаДѓдМга![]() жжзгЪЧВЛФмЗЂбПЕФМДПЩЃЎ
жжзгЪЧВЛФмЗЂбПЕФМДПЩЃЎ
ЂйжжзгИіЪ§ЪЧ700ЪБЃЌЗЂбПжжзгЕФИіЪ§ЪЧ624ЃЎЫљвджжзгЗЂбПЕФИХТЪДѓдМЪЧ0.891ЃЛЙЪДэЮѓЃЛ
ЂкЫцзХВЮМгЪЕбщЕФжжзгЪ§СПЕФдіМгЃЌЗЂбПжжзгЕФЦЕТЪдк0.9ИННќАкЖЏЃЌЯдЪОГівЛЖЈЕФЮШЖЈадЃЎПЩвдЙРМЦжжзгЗЂбПЕФИХТЪдМЮЊ0.9(ОЋШЗЕН0.1)ЃЛЙЪе§ШЗЃЛ
ЂлЪЕбщЕФжжзгИіЪ§зюЖрЕФФЧДЮЪЕбщЕУЕНЕФЗЂбПжжзгЕФЦЕТЪВЛвЛЖЈЪЧжжзгЗЂбПЕФИХТЪЃЛ
ЂмШєгУЦЕТЪЙРМЦжжзгЗЂбПЕФИХТЪдМЮЊ0.9ЃЌдђПЩвдЙРМЦ![]() жжзгДѓдМга
жжзгДѓдМга![]() ЕФжжзгВЛФмЗЂбПЃЌЙЪе§ШЗЃЛ
ЕФжжзгВЛФмЗЂбПЃЌЙЪе§ШЗЃЛ
ЦфжаКЯРэЕФЪЧЂкЂмЃЌ
ЙЪбЁDЃЎ


 ПЮЬУШЋНтзжДЪОфЖЮЦЊеТЯЕСаД№АИ
ПЮЬУШЋНтзжДЪОфЖЮЦЊеТЯЕСаД№АИ ВНВНИпПкЫуЬтПЈЯЕСаД№АИ
ВНВНИпПкЫуЬтПЈЯЕСаД№АИ ЕуОІаТНЬВФШЋФмНтЖСЯЕСаД№АИ
ЕуОІаТНЬВФШЋФмНтЖСЯЕСаД№АИ аЁбЇНЬВФЭъШЋНтЖСЯЕСаД№АИ
аЁбЇНЬВФЭъШЋНтЖСЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГАрЁАЪ§бЇаЫШЄаЁзщЁБЖдКЏЪ§![]() ЕФЭМЯѓКЭаджЪНјааСЫЬНОПЃЌЬНОПЙ§ГЬШчЯТЃЌЧыВЙГфЭъећЃК
ЕФЭМЯѓКЭаджЪНјааСЫЬНОПЃЌЬНОПЙ§ГЬШчЯТЃЌЧыВЙГфЭъећЃК
ЃЈ1ЃЉздБфСПxЕФШЁжЕЗЖЮЇЪЧ ЃЛ
ЃЈ2ЃЉШчБэЪЧyгыxЕФМИзщЖдгІЪ§жЕЃК
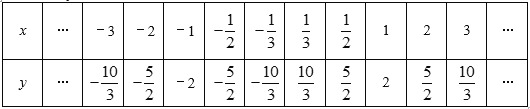
дкЦНУцжБНЧзјБъЯЕжаЃЌУшГіСЫвдБэжаИїЖдЖдгІжЕЮЊзјБъЕФЕуЃЌИљОнУшГіЕФЕуЃЌЛГіИУКЏЪ§ЕФЭМЯѓЃЛ
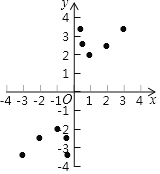
ЃЈ3ЃЉНјвЛВНЬНОПЗЂЯжЃКИУКЏЪ§дкЕквЛЯѓЯоФкЕФзюЕЭЕуЕФзјБъЪЧЃЈ1ЃЌ2ЃЉЃЌЙлВьКЏЪ§ЭМЯѓЃЌаДГіИУКЏЪ§ЕФСэвЛЬѕаджЪ ЃЛ
ЃЈ4ЃЉЧыФуРћгУХфЗНЗЈжЄУїЃКЕБxЃО0ЪБЃЌ![]() зюаЁжЕЮЊ2.ЃЈЬсЪОЃКЕБxЃО0ЪБ
зюаЁжЕЮЊ2.ЃЈЬсЪОЃКЕБxЃО0ЪБ![]() ЃЌ
ЃЌ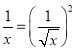 ЃЉ.
ЃЉ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌКЏЪ§![]() ЃЈ
ЃЈ![]() ЃЉЕФЭМЯѓОЙ§Еу
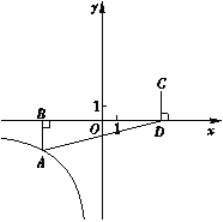
ЃЉЕФЭМЯѓОЙ§Еу![]() ЃЌABЁЭxжсгкЕуBЃЌЕуCгыЕуAЙигкдЕуOЖдГЦЃЌ CDЁЭxжсгкЕуDЃЌЁїABDЕФУцЛ§ЮЊ8.
ЃЌABЁЭxжсгкЕуBЃЌЕуCгыЕуAЙигкдЕуOЖдГЦЃЌ CDЁЭxжсгкЕуDЃЌЁїABDЕФУцЛ§ЮЊ8.
ЃЈ1ЃЉЧѓmЃЌnЕФжЕЃЛ
ЃЈ2ЃЉШєжБЯп![]() ЃЈkЁй0ЃЉОЙ§ЕуCЃЌЧвгыxжсЃЌyжсЕФНЛЕуЗжБ№ЮЊЕуEЃЌFЃЌЕБ
ЃЈkЁй0ЃЉОЙ§ЕуCЃЌЧвгыxжсЃЌyжсЕФНЛЕуЗжБ№ЮЊЕуEЃЌFЃЌЕБ![]() ЪБЃЌЧѓЕуFЕФзјБъЃЎ
ЪБЃЌЧѓЕуFЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбаОПЗЂЯжЃКГѕжабЇЩњЬ§ПЮЕФзЂвтСІжИБъЪ§ЪЧЫцзХРЯЪІНВПЮЪБМфЕФБфЛЏЖјБфЛЏЕФЃЎНВПЮПЊЪМЪБЃЌбЇЩњЕФзЂвтСІМЄдіЃЌжаМфгавЛЖЮЪБМфЃЌбЇЩњЕФзЂвтСІБЃГжЦНЮШзДЬЌЃЌЫцКѓПЊЪМЗжЩЂЃЎбЇЩњзЂвтСІжИБъЪ§![]() ЫцЪБМф
ЫцЪБМф![]() БфЛЏЕФКЏЪ§ЭМЯѓШчЭМЫљЪО(
БфЛЏЕФКЏЪ§ЭМЯѓШчЭМЫљЪО(![]() дНДѓБэЪОбЇЩњзЂвтСІдНМЏжа)ЃЎЕБ
дНДѓБэЪОбЇЩњзЂвтСІдНМЏжа)ЃЎЕБ![]() ЪБЃЌЭМЯѓЪЧХзЮяЯпЕФвЛВПЗжЃЛЕБ
ЪБЃЌЭМЯѓЪЧХзЮяЯпЕФвЛВПЗжЃЛЕБ![]() КЭ
КЭ![]() ЪБЃЌЭМЯѓЪЧЯпЖЮЃЎИљОнЭМЯѓЛиД№ЮЪЬтЃК
ЪБЃЌЭМЯѓЪЧЯпЖЮЃЎИљОнЭМЯѓЛиД№ЮЪЬтЃК
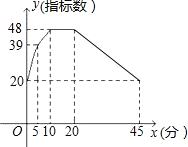
(1)ПЮЬУЩЯЃЌбЇЩњзЂвтСІБЃГжЦНЮШзДЬЌЕФЪБМфЖЮЪЧ_______ЃЎ
(2)НсКЯКЏЪ§ЭМЯѓЛиД№ЃЌвЛЕРМИКЮзлКЯЬтШчЙћашвЊНВ25ЗжжгЃЌРЯЪІзюКУдкЩЯПЮКѓДѓдМЕк______ЗжжгЕНЕк________ЗжжгНВетЕРЬтЃЌФмЪЙбЇЩњДІгкзЂвтСІБШНЯМЏжаЕФЬ§ПЮзДЬЌЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
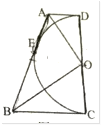
ЁОЬтФПЁПШчЭМЃЌвбжЊАыдВ![]() гыЫФБпаЮ
гыЫФБпаЮ![]() ЕФБп
ЕФБп![]() ЖМЯрЧаЃЌЧаЕуЗжБ№ЮЊ
ЖМЯрЧаЃЌЧаЕуЗжБ№ЮЊ![]() ЃЌАыОЖ
ЃЌАыОЖ![]() ЃЌдђ
ЃЌдђ![]() ___________.
___________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПББОЉЪРНчдАвеВЉРРЛс(МђГЦЁАЪРдАЛсЁБ)дАЧј4дТ29Шее§ЪНПЊдАЃЌУХЦБМлИёШчЯТЃК
ЦБжж | ЦБМл(дЊ/ШЫ) | |
жИЖЈШе | ЦеЭЈЦБ | 160 |
гХЛнЦБ | 100 | |
ЦНШе | ЦеЭЈЦБ | 120 |
гХЛнЦБ | 80 | |
зЂ1ЃКЁАжИЖЈШеЁБЮЊПЊдАШе(4дТ29Ше)ЁЂЮхвЛРЭЖЏНк(5дТ1Ше)ЁЂЖЫЮчНкЁЂжаЧяНкЁЂЪЎвЛМйЦк(КЌБедАШе)ЃЌЁАЦНШеЁБЮЊЪРдАЛсЛсЦкГ§ЁАжИЖЈШеЁБЭтЕФЦфЫћШеЦкЃЛ
зЂ2ЃКСљЪЎжмЫъМАвдЩЯРЯШЫЁЂЪЎАЫжмЫъвдЯТЕФбЇЩњОљПЩЙКТђгХЛнЦБЃЛ
зЂ3ЃКЬсЧАСНЬьМАвдЩЯдкЯпЩЯЙКТђЪРдАЛсУХЦБЃЌЦБМлПЩДђОХелЃЌЕЋНіЯогкЦеЭЈЦБЃЎ
ФГДѓМвЭЅМЦЛЎдк6дТ1ШеМЏЬхШыдАВЮЙлгЮРРЃЌЭЈЙ§МЦЫуЗЂЯжЃКШєЬсЧАСНЬьЯпЩЯЙКЦБЫљашЗбгУЮЊ996дЊЃЌЖјШыдАЕБЬьЙКЦБЫљашЗбгУЮЊ1080дЊЃЌдђИУМвЭЅжаПЩвдЙКТђгХЛнЦБЕФга______ШЫЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌЖдНЧЯпACЕФДЙжБЦНЗжЯпEFЗжБ№НЛADЁЂACЁЂBCгкЕуEЁЂOЁЂFЃЌСЌНгCEКЭAF.
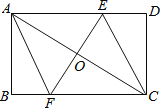
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮAECFЮЊСтаЮЃЛ
ЃЈ2ЃЉШєABЃН4ЃЌBCЃН8ЃЌЧѓСтаЮAECFЕФжмГЄ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
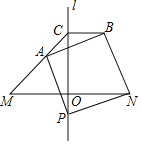
ЁОЬтФПЁПШчЭМЃЌжБЯпlЪЧЯпЖЮMNЕФДЙжБЦНЗжЯпЃЌНЛЯпЖЮMNгкЕуOЃЌдкMNЯТЗНЕФжБЯпlЩЯШЁвЛЕуPЃЌСЌНгPNЃЌвдЯпЖЮPNЮЊБпЃЌдкPNЩЯЗНзїе§ЗНаЮNPABЃЌЩфЯпMAНЛжБЯпlгкЕуCЃЌСЌНгBCЃЎ
ЃЈ1ЃЉЩшЁЯONPЃНІСЃЌЧѓЁЯAMNЕФЖШЪ§ЃЛ
ЃЈ2ЃЉаДГіЯпЖЮAMЁЂBCжЎМфЕФЕШСПЙиЯЕЃЌВЂжЄУїЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЖдгкЯпЖЮMNЕФЁАШ§ЕШЗжБфЛЛЁБЃЌИјГіШчЯТЖЈвхЃКШчЭМ1ЃЌЕуPЃЌQЮЊЯпЖЮMNЕФШ§ЕШЗжЕуЃЌМДMPЃНPQЃНQNЃЌНЋЯпЖЮPMвдЕуPЮЊа§зЊжааФЫГЪБеыа§зЊ90ЁуЕУЕНPMЁфЃЌНЋЯпЖЮQNвдЕуQЮЊа§зЊжааФЫГЪБеыа§зЊ90ЁуЕУЕНQNЁфЃЌдђГЦЯпЖЮMNНјааСЫШ§ЕШЗжБфЛЛЃЌЦфжаMЁфЃЌNЁфМЧЮЊЕуMЃЌNШ§ЕШЗжБфЛЛКѓЕФЖдгІЕу.
Р§ШчЃКШчЭМ2ЃЌЯпЖЮMNЃЌЕуMЕФзјБъЮЊЃЈ1ЃЌ5ЃЉЃЌЕуNЕФзјБъЮЊЃЈ1ЃЌ2ЃЉЃЌдђЕуPЕФзјБъЮЊЃЈ1ЃЌ4ЃЉЃЌЕуQЕФзјБъЮЊЃЈ1ЃЌ3ЃЉЃЌФЧУДЯпЖЮMNШ§ЕШЗжБфЛЛКѓЃЌПЩЕУЃКMЁфЕФзјБъЮЊЃЈ2ЃЌ4ЃЉЃЌЕуNЁфЕФзјБъЮЊЃЈ0ЃЌ3ЃЉ.
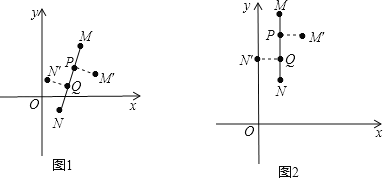
ЃЈ1ЃЉШєЕуPЕФзјБъЮЊЃЈ2ЃЌ0ЃЉЃЌЕуQЕФзјБъЮЊЃЈ4ЃЌ0ЃЉЃЌжБНгаДГіЕуMЁфгыЕуNЁфЕФзјБъЃЛ
ЃЈ2ЃЉШєЕуQЕФзјБъЪЧЃЈ0ЃЌЉ![]() ЃЉЃЌЕуPдкxжсе§АыжсЩЯЃЌЕуNЁфдкЕкЖўЯѓЯо.ЕБЯпЖЮPQЕФГЄЖШЮЊЗћКЯЬѕМўЕФзюаЁећЪ§ЪБЃЌЧѓOPЕФГЄЃЛ
ЃЉЃЌЕуPдкxжсе§АыжсЩЯЃЌЕуNЁфдкЕкЖўЯѓЯо.ЕБЯпЖЮPQЕФГЄЖШЮЊЗћКЯЬѕМўЕФзюаЁећЪ§ЪБЃЌЧѓOPЕФГЄЃЛ
ЃЈ3ЃЉШєЕуQЕФзјБъЮЊЃЈ0ЃЌ0ЃЉЃЌЕуMЁфЕФзјБъЮЊЃЈЉ3ЃЌЉ3ЃЉЃЌжБНгаДГіЕуPгыЕуNЕФзјБъЃЛ
ЃЈ4ЃЉЕуPЪЧвддЕуOЮЊдВаФЃЌ1ЮЊАыОЖЕФдВЩЯЕФвЛИіЖЈЕуЃЌЕуPЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЕБЕуNЁфдкдВOФкВПЛђдВЩЯЪБЃЌЧѓЯпЖЮPQЕФШЁжЕЗЖЮЇМАPQШЁзюДѓжЕЪБЕуMЁфЕФзјБъ.
ЃЉЕБЕуNЁфдкдВOФкВПЛђдВЩЯЪБЃЌЧѓЯпЖЮPQЕФШЁжЕЗЖЮЇМАPQШЁзюДѓжЕЪБЕуMЁфЕФзјБъ.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com