练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．计算：$\root{3}{-8}$+|$\sqrt{3}$-2|+$\sqrt{（-3）^{2}}$-（-$\sqrt{3}$）．

    分析 原式利用平方根、立方根定义，绝对值的代数意义计算即可得到结果．

    解答 解：原式=-2+2-$\sqrt{3}$+3+$\sqrt{3}$=3．

    点评 此题考查了实数的运算，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    8．选择适当方法解下列方程：
    （1）（x+1）2=2
    （2）x2-6x=4
    （3）2x2+3x-2=0
    （4）4x（2x-1）=3（2x-1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．小明、小华约好去滑雪场滑雪．小明乘环保车从民俗村出发，沿景区公路（如图1所示）去滑雪场，同时小华从古庙群出发，骑电动自行车沿景区公路去滑雪场．小明、小华与民俗村之间的路程s（单位：km）与时间t（单位：h）的函数图象如图2所示．
    （1）民俗村与古庙群之间的路程为10km；
    （2）分别求小明、小华与民俗村之间的路程s关于时间t的函数解析式（不要求写自变量的取值范围）；
    （3）直接写出当小明到达滑雪场时，小华与滑雪场的路程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图1，抛物线y=ax2+bx+$\frac{7}{4}$，经过A（1，0）、B（7，0）两点，交y轴于D点，以AB为边在x轴上方作等边△ABC．
    （1）求抛物线的解析式；
    （2）在x轴上方的抛物线上是否存在点M，是S△ABM=$\frac{4\sqrt{3}}{9}$S△ABC？若存在，请求出点M的坐标；若不存在，请说明理由；
    （3）如图2，E是线段AC上的动点，F是线段BC上的动点，AF与BE相交于点P．
    ①若CE=BF，试猜想AF与BE的数量关系及∠APB的度数，并说明理由；
    ②若AF=BE，当点E由A运动到C时，请直接写出点P经过的路径长（不需要写过程）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．计算：
    （1）（a-1）2-a（a-2）；               
    （2）（x-6）（x+4）+（3x+2）（2-3x）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．下列说法错误的是（　　）
    A．负数没有立方根B．一个正数有两个平方根
    C．0的立方根是0D．负数没有平方根

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

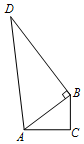    10．某机器零件呈四边形ACBD的形状，要求∠ABD=90°，∠C=90°．现测得∠ABD=90°，AD=39，BD=36，AC=12，BC=9．你认为这个零件合格吗？说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．小李到农贸批发市场了解到苹果和西瓜的价格信息如下：
    水果品种苹果西瓜
    批发价格8元/公斤1.6元/公斤
    零售价格10元/公斤2元/公斤
    他共用280元批发了苹果和西瓜共75公斤，
    （1）请问小李批发的苹果和西瓜各多少公斤？
    （2）若他当天把批发回来的苹果和西瓜按零售价格全部卖出，小李能赚多少钱？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

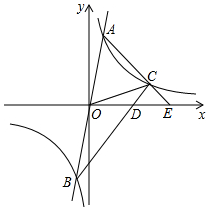    10．如图，双曲线y1=$\frac{k}{x}$与过原点的直线：y2=mx交于点A（1，4），B（-1，-4），
    （1）当y1＜y2时，x的取值范围是-1＜x＜0或x＞1；
    （2）点C是双曲线y1=$\frac{k}{x}$（x＞0）一点（不与A重合），直线AC、BC与x轴分别交于E、D；
    ①若OA=OC，则△CDE的面积为1
    ②若CE：CB=1：4，求△CDE的面积．

    查看答案和解析>>

    同步练习册答案