
����Ŀ����ͼ��������L1��y����x2��2x��3��x����A��B���㣬��y����M��������L1����ƽ��2����λ�õ�������L2��L2��x����C��D���㣮
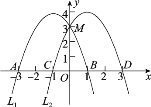
(1)��������L2��Ӧ�ĺ�������ʽ��
(2)������L1��L2��x���Ϸ��IJ����Ƿ���ڵ�N��ʹ��A��C��M��NΪ������ı�����ƽ���ı��Σ������ڣ������N�����ꣻ�������ڣ���˵�����ɣ�
(3)����P��������L1�ϵ�һ������(P�����A��B�غ�)����ô��P����ԭ��ĶԳƵ�Q�Ƿ���������L2�ϣ���˵�����ɣ�
���𰸡���1��y����x2��2x��3����2�����ڣ�N(2��3)��N��(��2��3);��3����Q����������L2�ϣ�
��������
(1)������ƽ�ƣ����������ߵĿ��ڷ���Ϳ��ڴ�С���䣬�����L1��x��Ľ��㣬�����L2��x��Ľ��㣬�������������L2�Ľ���ʽ��
(2)��Ϊ��ƽ�ƣ�����ƽ�Ƶ����ʣ����Ӹ����Ӧ����߶�ƽ������ȣ��ʴ��ڷ��������ĵ�N,�������N�����ꣻ
(3)�����L1�ϵĵ㣨x1��y1����������ù���ԭ��ĶԳƵ㣨-x1��-y1�����ٽ���-x1��-y1�����뺯��L2�Ľ���ʽ����������ͼ���ϣ�����������ͼ���ϣ�
�⣺(1)��y��0���ã�x2��2x��3��0��
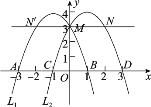
�� ��x1����3��x2��1��
�� ��A(��3��0)��B(1��0) ��
����������L1����ƽ��2����λ��������L2��
�� ��C(��1��0)��D(3��0)��a����1��
�� ��������L2Ϊy����(x��1)(x��3) ��
�� ��y����x2��2x��3��
(2)���ڣ���x��0����y��3��
��M(0��3),
����������L2��L1����ƽ��2����λ�õ��ģ�
�����N(2��3)��L2�ϣ���MN��2��MN��AC��
�֡�AC��2��
��MN��AC��
���ı���ACNMΪƽ���ı��Σ�
ͬ����L1�ϵĵ�N��(��2��3)����N��M��AC��N��M��AC��
�����ı���ACMN����ƽ���ı��Σ�
��N(2��3)��N��(��2��3)������
(3)��P(x1��y1)��L1������һ��(y1��0)��
���P����ԭ��ĶԳƵ�Q(��x1����y1)��
��![]() ��
��
����Q��������L2��
�ã�![]()
���Q����������L2�ϣ�


 �Ƹ������������ϵ�д�
�Ƹ������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
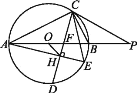
����Ŀ����ͼ,��ABC�ڽ��ڨ�O,AB�Ǩ�O��ֱ��,CDƽ�֡�ACB����O�ڵ�D,��AB�ڵ�F,��AE��CD�ڵ�H,����CE��OH.
(1)�ӳ�AB��Բ��һ��P,����PC,��PC2=PB��PA,��֤:PC�Ǩ�O������;
(2)��֤:CF��AE=AC��BC;
(3)��![]() =
=![]() ,��O�İ뾶��
,��O�İ뾶��![]() ,��tan��AEC��OH�ij�.
,��tan��AEC��OH�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
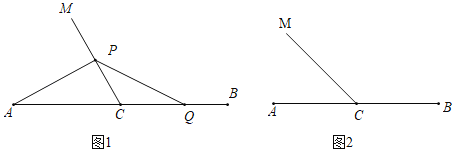
����Ŀ����֪CΪ�߶�AB�е㣬��ACM������QΪ�߶�BC��һ���㣨�����B�غϣ�����P������CM�ϣ�����PA��PQ����BQ��kCP��
��1��������60����k��1��
����ͼ1����QΪBC�е�ʱ�����PAC�Ķ�����
��ֱ��д��PA��PQ��������ϵ��
��2����ͼ2��������45��ʱ��̽���Ƿ���ڳ���k��ʹ�â��еĽ����Գ����������ڣ�д��k��ֵ��֤�����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С��ΪѧУ�ٰ����ѧ�Ļ���û�Ƶı�־���ڡ�ABC�У���ACB��90�����ԡ�ABC�ĸ���Ϊ�������������Σ���G����HI�ϣ���AC+BC��6�����Բ������Ϊ10.5������Ӱ�������Ϊ______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOB��45������OA�ϵ���O�ľ���ֱ�Ϊ1��3��5��7��9��11���ĵ���OA�Ĵ�����OB�ཻ���õ������һ���ɫ���Σ����ǵ�����ֱ�ΪS1��S2��S3��S4�������۲�ͼ�еĹ��ɣ������10����ɫ���ε����S10��_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ijУ���꼶������Ŀѵ��������Ӱ��꼶ѧ���������ȡ�˲���ѧ��������һ��������Ŀ���ԣ��Ѳ��Խ����Ϊ�ĸ��ȼ���A�������㣻B�������ã�C��������D�����������������Խ�����������������������ͳ��ͼ![]() �����ͳ��ͼ�е���Ϣ����������⣺
�����ͳ��ͼ�е���Ϣ����������⣺

��1��ͼ1��![]() �Ķ�����__________������ͼ2����ͳ��ͼ����������
�Ķ�����__________������ͼ2����ͳ��ͼ����������
��2����ȡ���ⲿ�ֵ�ѧ����������Ŀ���Խ������λ������__________����
��3�����ν����㡢���á����������Ϊ90�֡�80�֡�70�֡�50�֣�������ȡ���ⲿ��ѧ��������ƽ���ɼ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�ֱ��l1��y��k1x+b��A��0����3����B��5��2����ֱ��l2��y��k2x+2��
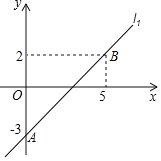
��1����ֱ��l1�ı���ʽ��
��2����x��4ʱ������ʽk1x+b��k2x+2���������д��һ�����������k2��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����֯ȫ���������100����ѡ�ֲμ����ܡ�����Ͷ��10���ᄊ��Ŀ��ɵġ�ʮ��ȫ�ܡ�����������25��ѡ�ֵ�һ�����ܳɼ���������Զ�ɼ�������10���ܳɼ������������ͼ��ʾ��
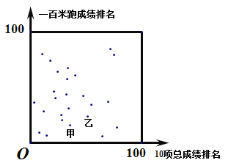
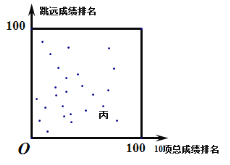
�ס��ҡ�����ʾ������ѡ�֣�������3���ƶϣ�
�ټ�һ�����ܳɼ�������10���ܳɼ�������ǰ�����ҵ�һ�����ܳɼ�������10���ܳɼ��������۱���һ�����ܳɼ���������Զ�ɼ�������ǰ��
���к������ǣ� ��
A.��B.��C.�٢�D.�٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�������꼶ѧ�������¹ڷ����������ڼ������п�������ѧϰЧ����ij��ѧ��ȡ�˲��ֲμӵ��в��Ե�ѧ���ɼ���Ϊ����������������Ϊ�š������С������࣬���Ƴ�������������������ͳ��ͼ�������ͼ���ṩ����Ϣ����������⣺
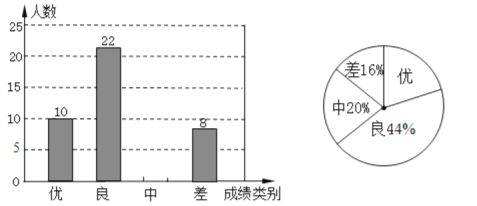
��1������ε����У�һ����ȡ�˶�����ѧ����
��2��ͨ�����㲹ȫ����ͳ��ͼ��
��3����У���꼶����320�˲μ�����ε��в��ԣ�������У���꼶���ж�����ѧ���ijɼ��ﵽ�����㣿
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com