
分析 (1)设每名熟练工和新工人每月分别可以安装x、y辆电动汽车.
根据“1名熟练工和2名新工人每月可安装8辆电动汽车”和“2名熟练工和3名新工人每月可安装14辆电动汽车”列方程组求解.
(2)设工厂有a名熟练工.根据新工人和抽调的熟练工刚好能完成一年的安装任务,根据a,m都是正整数和0<m<10,进行分析n的值的情况;
(3)建立函数关系式,根据使新工人的数量多于熟练工,同时工厂每月支出的工资总额W(元)尽可能地少,两个条件进行分析.
解答 解:(1)设每名熟练工和新工人每月分别可以安装x、y辆电动汽车.
根据题意,得:$\left\{\begin{array}{l}{x+2y=8}\\{2x+3y=14}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$.
答:每名熟练工和新工人每月分别可以安装4、2辆电动汽车.
(2)设工厂有a名熟练工.
根据题意,得12(4a+2m)=240,
2a+m=10,
m=10-2a,
又a,m都是正整数,0<m<10,
所以m=8,6,4,2.
即工厂有4种新工人的招聘方案.
①m=8,a=1,即新工人8人,熟练工1人;
②m=6,a=2,即新工人6人,熟练工2人;
③m=4,a=3,即新工人4人,熟练工3人;
④m=2,a=4,即新工人2人,熟练工4人.
(3)结合(2)知:要使新工人的数量多于熟练工,则m=8,a=1;或m=6,a=2;或m=4,a=3.
根据题意,得
W=8000a+4800n=8000a+4800(10-2a)=48000-1600a.
要使工厂每月支出的工资总额W(元)尽可能地少,则a应最大.
显然当m=4,a=3时,工厂每月支出的工资总额W(元)尽可能地少.
点评 本题主要考查二元一次方程组和二元一次方程的应用,解题的关键是要能够理解题意,正确找到等量关系和不等关系,熟练解方程组和根据条件分析不等式中未知数的值.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
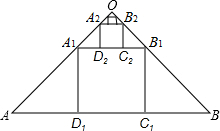 如图,在斜边长为1的等腰直角三角形OAB中,作内接正方形A1B1C1D1;在等腰直角三角形OA1B1中作内接正方形A2B2C2D2;在等腰直角三角形OA2B2中作内接正方形A3B3C3D3;…;依次作下去,则第2016个正方形A2016B2016C2016D2016的边长是$(\frac{1}{3})^{2016}$.
如图,在斜边长为1的等腰直角三角形OAB中,作内接正方形A1B1C1D1;在等腰直角三角形OA1B1中作内接正方形A2B2C2D2;在等腰直角三角形OA2B2中作内接正方形A3B3C3D3;…;依次作下去,则第2016个正方形A2016B2016C2016D2016的边长是$(\frac{1}{3})^{2016}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>b>c | B. | c>b>a | C. | b>c>a | D. | c>a>b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,三角形ABC中,∠C=90°,点D是AB上任意一点,∠CDE=∠ACD,DE交BC于点E.
如图,三角形ABC中,∠C=90°,点D是AB上任意一点,∠CDE=∠ACD,DE交BC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在压力不变的情况下,某物体承受的压强P(Pa)是它的受力面积S(m2)的反比例函数,其图象如图所示.
在压力不变的情况下,某物体承受的压强P(Pa)是它的受力面积S(m2)的反比例函数,其图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com