

 �����ռ��ּ����������µġ�ADE�͡�BDF�У��ֱ��ȡ�����Σ��õ�������ͬ�������Σ���Ϊ��2�μ�ȡ�����������������������Ϊ
�����ռ��ּ����������µġ�ADE�͡�BDF�У��ֱ��ȡ�����Σ��õ�������ͬ�������Σ���Ϊ��2�μ�ȡ�����������������������Ϊ (��ͼ2)����
(��ͼ2)���� ���������µ��ĸ��������У���ͬ�������ֱ��ȡ�����Σ��õ��ĸ���ͬ�������Σ���Ϊ��3�μ�ȡ���������ĸ������������Ϊ
���������µ��ĸ��������У���ͬ�������ֱ��ȡ�����Σ��õ��ĸ���ͬ�������Σ���Ϊ��3�μ�ȡ���������ĸ������������Ϊ ������������ȥ���������10�μ�ȡʱ��
������������ȥ���������10�μ�ȡʱ�� ��
�� ��
�� (3)
(3) 
 ��
��


 ��
�� ��
�� ����EC��MN��
����EC��MN�� ��
�� ��
��
 +��+
+��+ ��=
��=
 ��
�� ��
�� ��
�� �����˿�֪�����
�����˿�֪����� �����˹��ɿɵõ�10�μ�ȡ�����µ�����С�����ε����֮�ͣ�
�����˹��ɿɵõ�10�μ�ȡ�����µ�����С�����ε����֮�ͣ�


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
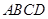 �У�
��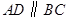 ��
��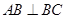 ��
��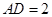 ��
��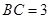 ��
��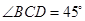 ������
������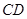 �Ե�
�Ե�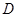 Ϊ������ʱ����ת
Ϊ������ʱ����ת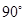 ��
��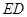 ������
������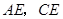 ����
����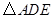 ������� ��
������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
| A��400+64; | B��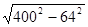 ; ; | C��400��64; | D�� |

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ?
?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
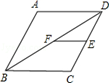
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 �У�
�� ��
�� ��
�� ��
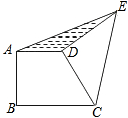
�� �ϵ�һ�㣬��ֱ��
�ϵ�һ�㣬��ֱ�� ��
�� �۵�����
�۵����� ǡ�����ڱ�
ǡ�����ڱ� ��һ��
��һ�� ������
������ ������������
������������ ���� ��
���� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
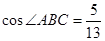 ����ô���¼�������
����ô���¼�������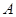 ��
��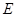 ֮��ľ���Ϊ cm��
֮��ľ���Ϊ cm��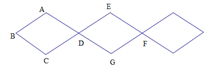
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com