
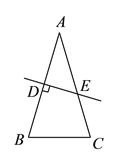
【题目】如图所示,等腰![]() 的周长为
的周长为![]() ,底边为
,底边为![]() ,
, ![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
(![]() )求
)求![]() 的周长;
的周长;
(![]() )若
)若![]() ,
, ![]() 为
为![]() 上一点,连结
上一点,连结![]() ,
, ![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)13;(2)![]() .
.
【解析】试题分析:(1)根据线段垂直平分线的定义得出AE=BE,则△BEC的周长转化为AE+EC+BC,即求AC+BC,则求出AC即可;(2)作点D关于AC的对称点F,连接AF,FP,BF,此时PD=PF,则DP+BP最小即为PF+BP最小,则当P、B、F共线时DP+BP最小,最小为线段BF的长,此时可求出∠BAF=60°,∠ABF=30°,则可得∠AFB=90°,根据勾股定理求解.
解:(1)∵等腰△ABC周长21,底边BC=5,
∴腰长AB=AC=(21-5)÷2=8,
∵DE为AB的垂直平分线,
∴AE=BE,
∴△BEC的周长为BE+EC+BC=AE+EC+BC=AC+BC=13.
(2)作点D关于AC的对称点F,连接AF,FP,BF,
则当P、B、F共线时DP+BP最小,最小为线段BF的长,
∵∠BAC=∠CAF=30°,
∴∠DAF=60°,且DA=DB=AF=4,
∴△ADF为等边三角形,
∴∠ADF=60°,DF=DB=4,
∴∠DBF=∠DFB=30°,
∴∠AFB=∠AFD+∠DFB=90°,
∴△ABF为直角三角形,,
∴BF=![]() =4
=4![]() ,
,
∴PD+BP最小值为![]() .
.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=4cm, BC=12cm.点P从点C处出发以1cm/s向A匀速运动,同时点Q从B点出发以2cm/s向C点匀速移动,若一个点到达目的停止运动时,另一点也随之停止运动.运动时间为t秒;

(1)用含有t的代数式表示BQ、CP的长;
(2)写出t的取值范围;
(3)用含有t的代数式 表示Rt△PCQ和四边形APQB的面积;
(4)当P、Q处在什么位置时,四边形PQBA的面积最小,并求这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某商品的进价为每件30元,九(1)班数学兴趣小组经过市场调查,整理出该商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
第x天 | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200-2x | |
(1)分别求出第25天和第60天商家在销售该商品时所获得的利润;
(2)问销售该商品第几天时,当天的销售利润为6050元?
查看答案和解析>>
科目:初中数学 来源: 题型:
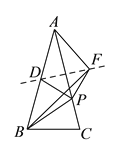
【题目】如图, ![]() 是等边三角形
是等边三角形![]() 内的一点,连结
内的一点,连结![]() 、
、![]() 、
、![]() ,以
,以![]() 为边作
为边作![]() 且
且![]() .连结
.连结![]() .
.
(1)观察并猜想![]() 与
与![]() 之间的大小关系,并证明你的结论.
之间的大小关系,并证明你的结论.
(2)若![]() ,
, ![]() ,
, ![]() ,连结
,连结![]() ,试判断
,试判断![]() 的形状,并说明理由.
的形状,并说明理由.
(3)在(2)的条件下,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形边长都是![]() ,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(![]() )画一个三角形,使它的三边长都是有理数.
)画一个三角形,使它的三边长都是有理数.
(![]() )画一个直角三角形,使它们的三边长都是无理数.
)画一个直角三角形,使它们的三边长都是无理数.
(![]() )画出与
)画出与![]() 成轴对称且与
成轴对称且与![]() 有公共点的格点三角形(画出一个即可).
有公共点的格点三角形(画出一个即可).



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2009年初甲型HIN1流感在墨西哥爆发并在全球蔓延,研究表明,甲型HIN1流感球形病毒细胞的直径约为0.00000156 m,用科学记数法表示这个数是( )
A. 0.156×10-5m B. 0.156×105m C. 1.56×10-6m D. 1.56×106m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com