
已知抛物线![]() .
.
⑴当a =-1时,求此抛物线的顶点坐标和对称轴;
⑵若代数式![]() 的值为正整数,求x的值;
的值为正整数,求x的值;
⑶当![]() 时,抛物线
时,抛物线![]() 与x轴的正半轴相交于点M(m,0);当
与x轴的正半轴相交于点M(m,0);当![]() 时,抛物线
时,抛物线![]() 与x轴的正半轴交于点N(n,0).若点M在点N的左边,试比较
与x轴的正半轴交于点N(n,0).若点M在点N的左边,试比较![]() 与
与![]() 的大小.
的大小.
解:(1)方法一:
当![]() =-1时,
=-1时,
![]()
=![]()
∴抛物线的顶点坐标为(![]() ,
,![]() ),对称轴为直线
),对称轴为直线![]() =
=![]()
方法二:
当![]() =-1时,
=-1时,![]() ,∴
,∴![]() =-1,b=1,c=2.
=-1,b=1,c=2.
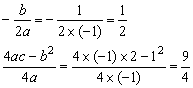
∴抛物线的顶点坐标为(![]() ),对称轴为直线
),对称轴为直线![]() .
.
(2) ∵代数式![]() 的值为正整数,∴函数
的值为正整数,∴函数![]() 的值为正整数.
的值为正整数.
又∵函数的最大值为![]() ,∴
,∴![]() 的正整数值只能为1或2
的正整数值只能为1或2
当![]() =-1时,
=-1时,![]() =1,解得
=1,解得![]()
当![]() =2时,
=2时,![]() =2,解得
=2,解得![]()
∴![]() 的值为
的值为![]() 、0或1
、0或1
(3)方法一:
∵当![]() =
= ![]() 1时,抛物线
1时,抛物线![]() 过
过![]() 轴正半轴上的点M(m,0)
轴正半轴上的点M(m,0)
∴![]()
![]() ,
,
∴![]() .
.
同理![]()
![]()
=![]()
=![]()
=![]()
又∵点M、N在x轴正半轴上,且点M在点N的左边,
∴0<m<n,∴m-n<0, ∴![]() <0.
<0.
即![]()
方法二:
抛物线![]() 的对称轴为
的对称轴为![]()
∴当![]() >0时,
>0时,![]()
此时抛物线![]() 的对称轴在
的对称轴在![]() 轴的左侧
轴的左侧
又∵抛物线![]() 与
与![]() 轴相交于(0,2),
轴相交于(0,2),
∴抛物线![]() 与
与![]() 轴的正半轴无交点。
轴的正半轴无交点。
∴当![]() >0不合题意。
>0不合题意。
当![]()
![]() 0时,即
0时,即![]()
经过点M的抛物线![]() 的对称轴为
的对称轴为![]() ,
,
经过点N的抛物线![]() 的对称轴为
的对称轴为![]() ,
,
∵点M在点N的左边,且抛物线经过点(0,2)(此时两条抛物线如图所示)
 ∴直线
∴直线![]() 在直线
在直线![]() 的左侧,
的左侧,
∴![]() ,∴
,∴![]()


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
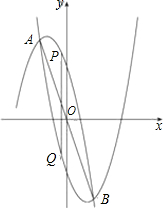 已知抛物线y=-x2-3x+4和抛物线y=x2-3x-4相交于A,B两点.点P在抛物线C1上,且位于点A和点B之间;点Q在抛物线C2上,也位于点A和点B之间.
已知抛物线y=-x2-3x+4和抛物线y=x2-3x-4相交于A,B两点.点P在抛物线C1上,且位于点A和点B之间;点Q在抛物线C2上,也位于点A和点B之间.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知抛物线y=
已知抛物线y=| 1 |
| 2 |
| 7 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 | MQ |

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知抛物线y1=-3x2+3,直线y2=3x+3,当x任取一值时,x对应的函数值分别为y1,y2.若y1≠y2,取y1,y2中的较小值记为M;若y1=y2,记M=y1=y2.下列判断:
如图,已知抛物线y1=-3x2+3,直线y2=3x+3,当x任取一值时,x对应的函数值分别为y1,y2.若y1≠y2,取y1,y2中的较小值记为M;若y1=y2,记M=y1=y2.下列判断:| 2 |
| 3 |
| ||
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:044
(2007,辽宁省大连市,24)已知抛物线 .
.
(1)当a=-1时,求此抛物线的顶点坐标和对称轴;
(2)若代数式 的值为正整数,求x的值;
的值为正整数,求x的值;
(3)当 时,抛物线
时,抛物线 与x轴的正半轴相交于点M(m,0);当
与x轴的正半轴相交于点M(m,0);当 时,抛物线
时,抛物线 与x轴的正半轴相交于点N(n,0).若点M在点N的左边,试比较
与x轴的正半轴相交于点N(n,0).若点M在点N的左边,试比较 与
与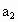 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com