
【题目】如图,在矩形ABCD中,AB=4,BC=5,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE.延长AF交边BC于点G,则CG为_____.

【答案】![]()
【解析】
如图,作辅助线,首先证明△EFG≌△ECG,得到FG=CG(设为x ),∠FEG=∠CEG;同理可证AF=AD=5,∠FEA=∠DEA,进而证明△AEG为直角三角形,运用相似三角形的性质即可解决问题.
连接EG;
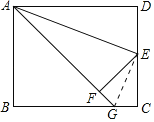
∵四边形ABCD为矩形,
∴∠D=∠C=90°,DC=AB=4;
由题意得:EF=DE=EC=2,∠EFG=∠D=90°;
在Rt△EFG与Rt△ECG中,
![]() ,
,
∴Rt△EFG≌Rt△ECG(HL),
∴FG=CG(设为x ),∠FEG=∠CEG;
同理可证:AF=AD=5,∠FEA=∠DEA,
∴∠AEG=![]() ×180°=90°,
×180°=90°,
而EF⊥AG,可得△EFG∽△AFE,
∴![]()
∴22=5x,
∴x=![]() ,
,
∴CG=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,DB=DC,∠BAC=∠BDC=120°,DM⊥AC,E为BA延长线上的点,∠BAC的角平分线交BC于N,∠ABC的外角平分线交CA的延长线于点P,连接PN交AB于K,连接CK,则下列结论正确的是:①∠ABD=∠ACD;②DA平分∠EAC;③当点A在DB左侧运动时,![]() 为定值;④∠CKN=30° ( )
为定值;④∠CKN=30° ( )
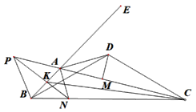
A.①③④B.②③④C.①②④D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李对某班全体同学的业余兴趣爱好进行了一次调查,根据采集到的数据绘制了下面的统计图表.请据图中提供的信息,解答下列问题:


(1)该班共有学生_____________人;
(2)在图1中,请将条形统计图补充完整;
(3)在图2中,在扇形统计图中,“音乐”部分所对应的圆心角的度数___________度:
(4)求爱好“书画”的人数占该班学生数的百分数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,面积为4的正方形OABC的顶点O与坐标原点重合,边OA、OC分别在x轴、y轴的正半轴上,点B、P都在函数y=![]() (x>0)的图象上,过动点P分别作轴x、y轴的平行线,交y轴、x轴于点D、E.设矩形PDOE与正方形OABC重叠部分图形的面积为S,点P的横坐标为m.
(x>0)的图象上,过动点P分别作轴x、y轴的平行线,交y轴、x轴于点D、E.设矩形PDOE与正方形OABC重叠部分图形的面积为S,点P的横坐标为m.
(1)求k的值;
(2)用含m的代数式表示CD的长;
(3)求S与m之间的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
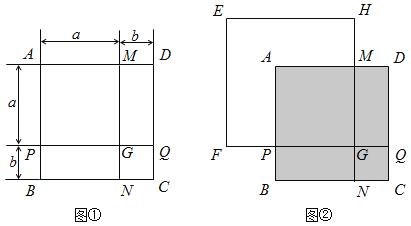
【题目】如图①,正方形ABCD是由两个长为a、宽为b的长方形和两个边长分别为a、b的正方形拼成的.
(1)利用正方形ABCD面积的不同表示方法,直接写出![]() 、
、![]() 、ab之间的关系式,这个关系式是 ;
、ab之间的关系式,这个关系式是 ;
(2)若m满足![]() ,请利用(1)中的数量关系,求
,请利用(1)中的数量关系,求![]() 的值;
的值;
(3)若将正方形EFGH的边![]() 、
、![]() 分别与图①中的PG、MG重叠,如图②所示,已知PF=8,NH=32,求图中阴影部分的面积(结果必须是一个具体数值).
分别与图①中的PG、MG重叠,如图②所示,已知PF=8,NH=32,求图中阴影部分的面积(结果必须是一个具体数值).
查看答案和解析>>
科目:初中数学 来源: 题型:
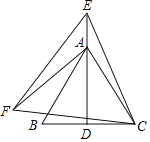
【题目】如图,D为等边△ABC中边BC的中点,在边DA的延长线上取一点E,以CE为边、在CE的左下方作等边△CEF,连结AF.若AB=4,AF=![]() ,则CF的值为_____.
,则CF的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABE与△CDE都是等腰直角三角形,∠AEB=∠DEC=90°,连接AD,AC,BC,BD,若AD=AC=AB,则下列结论:①AE垂直平分CD,②AC平分∠BAD,③△ABD是等边三角形,④∠BCD的度数为150°,其中正确的个数是( )

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中以点A为圆心,AB为半径作圆A交网格于点C(如图(1)),过点C作圆的切线交网格于点D,以点A为圆心,AD为半径作圆交网格于点E(如图(2)).
问题:
(1)求∠ABC的度数;
(2)求证:△AEB≌△ADC;
(3)△AEB可以看作是由△ADC经过怎样的变换得到的?并判断△AED的形状(不用说明理由).
(4)如图(3),已知直线a,b,c,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形A′B′C′使三个顶点A′,B′,C′,分别在直线a,b,c上.要求写出简要的画图过程,不需要说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)解方程: ![]() ;
;
(2)已知关于x的一元二次方程(a+c)x2+2bx+(a-c)=0,其中a,b,c分别为△ABC三边的长.
①如果x=-1是方程的根,试判断△ABC的形状,并说明理由;
②如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
③如果△ABC是等边三角形,试求这个一元二次方程的根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com