

分析 (1)△ABC的面积=3×3-1×2÷2-1×3÷2-2×3÷2=$\frac{7}{2}$;
(2)$\sqrt{5}$a是直角边长为a,2a的直角三角形的斜边;$\sqrt{8}$a是直角边长为2a,2a的直角三角形的斜边;$\sqrt{17}$a是直角边长为a,4a的直角三角形的斜边,把它整理为一个矩形的面积减去三个直角三角形的面积;
(3)结合(1),(2)易得此三角形的三边分别是直角边长为m,4n的直角三角形的斜边;直角边长为3m,2n的直角三角形的斜边;直角边长为4m,2n的直角三角形的斜边.同样把它整理为一个矩形的面积减去三个直角三角形的面积.
解答 解:(1)S△ABC=3×3-$\frac{1}{2}$×1×2-$\frac{1}{2}$×1×3-$\frac{1}{2}$×2×3=$\frac{7}{2}$.
故答案为:$\frac{7}{2}$.
(2)如图1,在边长为a的正方形网格中,△ABC即为所求作三角形,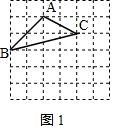
S△ABC=2a×4a-$\frac{1}{2}$×2a×2a-$\frac{1}{2}$×2a×a-$\frac{1}{2}$×4a×a=3a2;
(3)如图2,在长为m、宽为n的网格中,△ABC即为所求作三角形,
其中AB=$\sqrt{{m}^{2}+16{n}^{2}}$、AC=$\sqrt{9{m}^{2}+4{n}^{2}}$、BC=$\sqrt{16{m}^{2}+4{n}^{2}}$,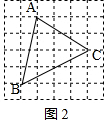
S△ABC=4m×4n-$\frac{1}{2}$×m×4n-$\frac{1}{2}$×3m×2n-$\frac{1}{2}$×4m×2n=7mn.
点评 此题主要考查了勾股定理应用,利用了数形结合的思想,通过构造直角三角形,利用勾股定理求解是解题关键.关键是结合网格用矩形及容易求得面积的直角三角形表示出所求三角形的面积进行解答.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:填空题
 在△ABC中,AC=BC,BD⊥AC,交AC边的延长线于点D,点E在AB边上,EF⊥BD于点F,且EF=BD,若AC=$\frac{13}{4}$,DF=1(BF>CD),则线段BE的长为$\sqrt{13}$.
在△ABC中,AC=BC,BD⊥AC,交AC边的延长线于点D,点E在AB边上,EF⊥BD于点F,且EF=BD,若AC=$\frac{13}{4}$,DF=1(BF>CD),则线段BE的长为$\sqrt{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在长方形ABCD中无重叠放入面积分别为16cm2和12cm2的两张正方形纸片,则图中空白部分的面积为( )cm2.
如图,在长方形ABCD中无重叠放入面积分别为16cm2和12cm2的两张正方形纸片,则图中空白部分的面积为( )cm2.| A. | 16-8$\sqrt{3}$ | B. | -12+8$\sqrt{3}$ | C. | 8-4$\sqrt{3}$ | D. | 4-2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
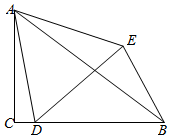 在Rt△ACB中,∠ACB=90°,点D在边BC上,连接AD,以点D为顶点,AD为一边作等边△ADE,连接BE,若BC=7,BE=4,∠CBE=60°,则∠EAB的正切值为$\frac{2\sqrt{3}}{11}$.
在Rt△ACB中,∠ACB=90°,点D在边BC上,连接AD,以点D为顶点,AD为一边作等边△ADE,连接BE,若BC=7,BE=4,∠CBE=60°,则∠EAB的正切值为$\frac{2\sqrt{3}}{11}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
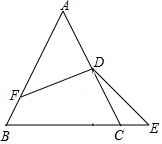 已知△ABC是等边三角形,D是AC的中点,F为AB边上一点,且AF=2BF,E为射线BC上一点,∠EDF=120°,则$\frac{CE}{CD}$=$\frac{1}{3}$.
已知△ABC是等边三角形,D是AC的中点,F为AB边上一点,且AF=2BF,E为射线BC上一点,∠EDF=120°,则$\frac{CE}{CD}$=$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知等腰△ABC中,AB=AC=5a,BC=8a.点D、E为边AB、BC上两点.
已知等腰△ABC中,AB=AC=5a,BC=8a.点D、E为边AB、BC上两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com