
分析 (1)设点A关于点B的对称点为点C为m,再根据A、C两点到B点的距离相等即可求解;
(2)因为1<$\sqrt{2}$<2,所以a的整数部分为1,所以4<6-$\sqrt{2}$<5,由此求得c小数部分,然后代入代数式即可.
解答 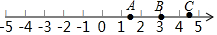 解:(1)设点A关于点B的对称点为点C,
解:(1)设点A关于点B的对称点为点C,
则$\frac{\sqrt{2}+m}{2}$=3,
解得m=6-$\sqrt{2}$;
故C点所对应的数为:6-$\sqrt{2}$;
(2)∵1<$\sqrt{2}$<2,
∴a的整数部分为x=1,4<6-$\sqrt{2}$<5,
所以6-$\sqrt{2}$的整数部分是4,小数部分y=6-$\sqrt{2}$-4=2-$\sqrt{2}$,
∴2x3+2y=2×13+2×(2-$\sqrt{2}$)=6-2$\sqrt{2}$.
点评 本题考查的是实数与数轴,无理数的估算,任意一个实数都可以用数轴上的点表示;反之,数轴上的任意一个点都表示一个实数;无理数的估算注意找出最接近的整数范围.


科目:初中数学 来源: 题型:解答题
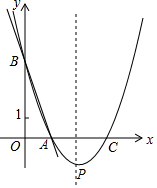 如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=(x-h)2+k经过点A、B,其顶点为P.在抛物线的对称轴上是否存在一点Q,连接QA、QB,并将△ABQ沿AB翻折,得到菱形AQBQ′?若存在,请求出点Q的坐标;若不存在,说明理由.
如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=(x-h)2+k经过点A、B,其顶点为P.在抛物线的对称轴上是否存在一点Q,连接QA、QB,并将△ABQ沿AB翻折,得到菱形AQBQ′?若存在,请求出点Q的坐标;若不存在,说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
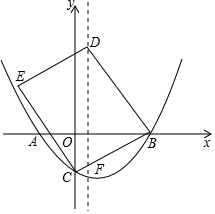 如图,抛物线y═ax2+bx+c交x轴于点A,B(点A在x轴的负半轴,点B在x轴的正半轴),交y轴的负半轴于点C,且OA=OC=$\frac{1}{2}$BO=k(k>0).点D在抛物线的对称轴上,BC交对称轴于点F.
如图,抛物线y═ax2+bx+c交x轴于点A,B(点A在x轴的负半轴,点B在x轴的正半轴),交y轴的负半轴于点C,且OA=OC=$\frac{1}{2}$BO=k(k>0).点D在抛物线的对称轴上,BC交对称轴于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com