
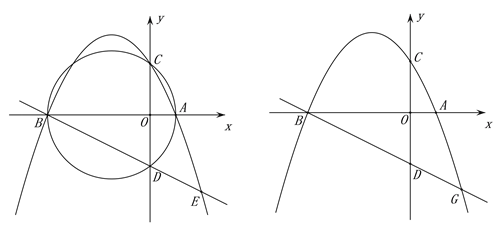
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖÅ×ĪļĻßy£½£![]() x2£«bx£«c½»xÖįÓŚµćA(2£¬0)”¢B£ØŅ»8£¬0£©£¬½»yÖįÓŚµćC£¬¹żµćA”¢B”¢CČżµćµÄ”ŃMÓėyÖįµÄĮķŅ»øö½»µćĪŖD£®
x2£«bx£«c½»xÖįÓŚµćA(2£¬0)”¢B£ØŅ»8£¬0£©£¬½»yÖįÓŚµćC£¬¹żµćA”¢B”¢CČżµćµÄ”ŃMÓėyÖįµÄĮķŅ»øö½»µćĪŖD£®
(1)Ēó“ĖÅ×ĪļĻߵıķ“ļŹ½¼°Ō²ŠÄMµÄ×ų±ź£»
(2)ÉčPĪŖ»”BCÉĻČĪŅāŅ»µć£Ø²»ÓėµćB£¬CÖŲŗĻ£©£¬Į¬½ÓAP½»yÖįÓŚµćN£¬ĒėĪŹ£ŗAP”¤ANŹĒ·ńĪŖ¶ØÖµ£¬ČōŹĒ£¬ĒėĒó³öÕāøöÖµ£»Čō²»ŹĒ£¬ĒėĖµĆ÷ĄķÓÉ£»
(3)ŃÓ³¤Ļ߶ĪBD½»Å×ĪļĻßÓŚµćE£¬ÉčµćFŹĒĻ߶ĪBEÉĻµÄČĪŅāŅ»µć£Ø²»ŗ¬¶Ėµć£©£¬Į¬½ÓAF£®¶ÆµćQ“ÓµćA³ö·¢£¬ŃŲĻ߶ĪAFŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČŌĖ¶Æµ½µćF£¬ŌŁŃŲĻ߶ĪFBŅŌĆæĆė![]() øöµ„Ī»µÄĖŁ¶ČŌĖ¶Æµ½µćBŗóĶ£Ö¹£¬ĪŹµ±µćFµÄ×ų±źŹĒ¶ąÉŁŹ±£¬µćQŌŚÕūøöŌĖ¶Æ¹żńĪÖŠĖłÓĆŹ±¼ä×īÉŁ£æ
øöµ„Ī»µÄĖŁ¶ČŌĖ¶Æµ½µćBŗóĶ£Ö¹£¬ĪŹµ±µćFµÄ×ų±źŹĒ¶ąÉŁŹ±£¬µćQŌŚÕūøöŌĖ¶Æ¹żńĪÖŠĖłÓĆŹ±¼ä×īÉŁ£æ
”¾“š°ø”æ£Ø1£©M(£3,0) £Ø2£©¶ØÖµŹĒ20 £Ø3£©F(£2,£3)
”¾½āĪö”æ(1)”¢øł¾ŻµćAŗĶµćBµÄ×ų±źµĆ³öŗÆŹż½āĪöŹ½£¬“Ó¶ųµĆ³öµćCµÄ×ų±źŅŌ¼°AB”¢ACŗĶBCµÄ³¤¶Č£¬“Ó¶ųµĆ³ö”÷ABCĪŖÖ±½ĒČż½ĒŠĪ£¬øł¾ŻŌ²µÄŠŌÖŹµĆ³öµćMµÄ×ų±ź£»(2)”¢øł¾ŻĢāŅāµĆ³ö”÷APBŗĶ”÷AONĻąĖĘ£¬“Ó¶ųµĆ³ö“š°ø£»(3)”¢¹żµćBŌŚBEµÄĻĀĆę×÷ÉäĻßBI£¬½»yÖįÓŚµćI£¬¹żµćA×öAH”ĶBI£¬“¹×ćĪŖµćH,ÓėÉäĻßBEµÄ½»µć¼“ĪŖŌĖ¶ÆŹ±¼ä×īÉŁŹ±µćFµÄĪ»ÖĆ£¬¹żµćD×öDK”ĶBI£¬“¹×ćĪŖK£¬øł¾Ż¹“¹É¶ØĄķµĆ³öµćIµÄ×ų±ź£¬“Ó¶ųµĆ³öBIŗĶAHµÄŗÆŹż±ķ“ļŹ½£¬øł¾Ż½»µćĪŹĢāĮŠ³ö·½³ĢµĆ³öµćFµÄ×ų±ź£®
(1)”¢½«A£Ø2£¬0£©”¢B£Ø£8£¬0£©Į½µć“śČė![]() µĆ£ŗ
µĆ£ŗ![]() £¬
£¬
½āµĆ£ŗ![]() £¬”ąÅ×ĪļĻߵıķ“ļŹ½ĪŖ£ŗ
£¬”ąÅ×ĪļĻߵıķ“ļŹ½ĪŖ£ŗ![]() £¬”ą C(0£¬4)£¬
£¬”ą C(0£¬4)£¬
”ą BC£½4![]() £¬ AC£½2
£¬ AC£½2![]() £¬AB£½10£¬ ”ą”÷ABCĪŖÖ±½ĒČż½ĒŠĪ,ĒŅ”ĻACB£½90”ć£¬
£¬AB£½10£¬ ”ą”÷ABCĪŖÖ±½ĒČż½ĒŠĪ,ĒŅ”ĻACB£½90”ć£¬
”ß”ĻACB£½90”ć£¬ ”ąABĪŖÖ±¾¶£¬ ”ąM(£3£¬0)£»
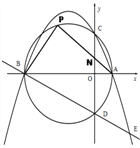
(2)”¢ČēĶ¼: ”ßABĪŖÖ±¾¶£¬ ”ą”ĻAPB£½90”ć£¬ ”ß”ĻAPB£½”ĻAON, ”ĻNAO£½”ĻBAP£¬
”ą”÷APB”×”÷AON£¬”ą![]() £¬ ”ąAN”¤AP£½AB”¤AO£½20£¬”ąĪŖ¶ØÖµ,¶ØÖµŹĒ20£®
£¬ ”ąAN”¤AP£½AB”¤AO£½20£¬”ąĪŖ¶ØÖµ,¶ØÖµŹĒ20£®
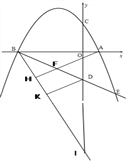
(3)”¢¹żµćBŌŚBEµÄĻĀĆę×÷ÉäĻßBI£¬½»yÖįÓŚµćI£¬
¹żµćA×öAH”ĶBI£¬“¹×ćĪŖµćH,ÓėÉäĻßBEµÄ½»µć¼“ĪŖŌĖ¶ÆŹ±¼ä×īÉŁŹ±µćFµÄĪ»ÖĆ£¬
¹żµćD×öDK”ĶBI£¬“¹×ćĪŖK£¬ ”ßBEĘ½·Ö”ĻABI£¬”ąDI£½DO£½4£¬BO£½BK£½8£¬
ÉčDI£½x,ŌņKI£½2x£8£¬ ”ą16£«![]() £½
£½![]() £¬
£¬ ![]() (ÉįČ„)£¬
(ÉįČ„)£¬
”ąI(0£¬![]() ) £¬ ”ąBI±ķ“ļŹ½ĪŖ:
) £¬ ”ąBI±ķ“ļŹ½ĪŖ:![]() £¬ ”ąAH±ķ“ļŹ½ĪŖ
£¬ ”ąAH±ķ“ļŹ½ĪŖ![]() £¬
£¬
”ßBD±ķ“ļŹ½ĪŖ![]() £¬ ”ą
£¬ ”ą![]() £¬ ”ą£½£2£¬ ”ąF(£2£¬£3) £®
£¬ ”ą£½£2£¬ ”ąF(£2£¬£3) £®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖy¹ŲÓŚxµÄ¶ž“ĪŗÆŹży=ax2©bx+2£Øa”Ł0£©£®
£Ø1£©µ±a=©2£¬b=©4Ź±£¬ĒóøĆŗÆŹżĶ¼ĻóµÄ¶Ō³ĘÖį¼°¶„µć×ų±ź£®
£Ø2£©ŌŚ£Ø1£©µÄĢõ¼žĻĀ£¬Q£Øm£¬t£©ĪŖøĆŗÆŹżĶ¼ĻóÉĻµÄŅ»µć£¬ČōQ¹ŲÓŚŌµćµÄ¶Ō³ĘµćPŅ²ĀäŌŚøĆŗÆŹżĶ¼ĻóÉĻ£¬ĒómµÄÖµ£®
£Ø3£©µ±øĆŗÆŹżĶ¼Ļó¾¹żµć£Ø1£¬0£©Ź±£¬ČōA£Ø![]() £¬y1£©£¬B£Ø
£¬y1£©£¬B£Ø![]() £¬y2£©ŹĒøĆŗÆŹżĶ¼ĻóÉĻµÄĮ½µć£¬ŹŌ±Č½Ļy1Óėy2µÄ“󊔣®
£¬y2£©ŹĒøĆŗÆŹżĶ¼ĻóÉĻµÄĮ½µć£¬ŹŌ±Č½Ļy1Óėy2µÄ“󊔣®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¶ž“ĪŗÆŹż![]() µÄĶ¼ĻóÓė
µÄĶ¼ĻóÓė![]() Öį½»ÓŚµć
Öį½»ÓŚµć![]() ”¢
”¢![]() £¬ĒŅ
£¬ĒŅ![]() £¬Óė
£¬Óė![]() ÖįµÄÕż°ėÖįµÄ½»µćŌŚ
ÖįµÄÕż°ėÖįµÄ½»µćŌŚ![]() µÄĻĀ·½£®ĻĀĮŠ½įĀŪ£ŗ¢Ł
µÄĻĀ·½£®ĻĀĮŠ½įĀŪ£ŗ¢Ł![]() £»¢Ś
£»¢Ś![]() £»¢Ū
£»¢Ū![]() £»¢Ü
£»¢Ü![]() £®ĘäÖŠÕżČ·½įĀŪµÄøöŹżŹĒ£Ø £©øö£®
£®ĘäÖŠÕżČ·½įĀŪµÄøöŹżŹĒ£Ø £©øö£®
A. 4øö B. 3øö C. 2øö D. 1øö
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼Īäæ×¼±øĶź³ÉĢāÄæ£ŗ»Æ¼ņ£ŗ![]() £¬·¢ĻÖĻµŹż”°
£¬·¢ĻÖĻµŹż”°![]() ”±Ó”Ė¢²»Ē峞£®
”±Ó”Ė¢²»Ē峞£®
£Ø1£©Ėū°Ń”°![]() ”±²Ā³É3£¬ĒėÄć»Æ¼ņ£ŗ£Ø3x2+6x+8£©ØC£Ø6x+5x2+2£©£»
”±²Ā³É3£¬ĒėÄć»Æ¼ņ£ŗ£Ø3x2+6x+8£©ØC£Ø6x+5x2+2£©£»
£Ø2£©ĖūĀčĀčĖµ£ŗ”°Äć²Ā“ķĮĖ£¬ĪŅ擵½øĆĢā±ź×¼“š°øµÄ½į¹ūŹĒ³£Źż£®”±Ķعż¼ĘĖćĖµĆ÷ŌĢāÖŠ”°![]() ”±ŹĒ¼ø£æ
”±ŹĒ¼ø£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬½×ĢŻĶ¼µÄĆæøöĢؽ×ÉĻ¶¼±ź×ÅŅ»øöŹż£¬“ÓĻĀµ½ÉĻµÄµŚ1øöÖĮµŚ4øöĢؽ×ÉĻŅĄ“Ī±ź×Å©5£¬©2£¬1£¬9£¬ĒŅČĪŅāĻąĮŚĖÄøöĢؽ×ÉĻŹżµÄŗĶ¶¼ĻąµČ£®
³¢ŹŌ £Ø1£©ĒóĒ°4øöĢؽ×ÉĻŹżµÄŗĶŹĒ¶ąÉŁ£æ
£Ø2£©ĒóµŚ5øöĢؽ×ÉĻµÄŹżxŹĒ¶ąÉŁ£æ
Ó¦ÓĆ Ēó“ÓĻĀµ½ÉĻĒ°31øöĢؽ×ÉĻŹżµÄŗĶ£®
·¢ĻÖ ŹŌÓĆŗ¬k£ØkĪŖÕżÕūŹż£©µÄŹ½×Ó±ķŹ¾³öŹż”°1”±ĖłŌŚµÄĢØ½×Źż£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŹżŃ§Š”×éµÄĶ¬Ń§ĪŖĮĖ½āѧɜĆæÖÜŌĶĮµÄŹ±¼ä£¬Ė껜µ÷²éĮĖ50ĆūĶ¬Ń§£¬»ęÖĘĮĖČēĶ¼ĖłŹ¾µÄĶ³¼ĘĶ¼£¬Õā×鏿¾ŻµÄÖŠĪ»ŹżŗĶÖŚŹż·Ö±šŹĒ£Ø””””£©
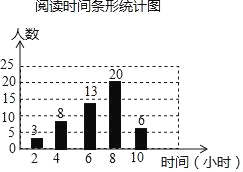
A. ÖŠĪ»ŹżŹĒ25ČĖ£¬ÖŚŹżŹĒ20ČĖ B. ÖŠĪ»ŹżŗĶÖŚŹż¶¼ŹĒ8Š”Ź±
C. ÖŠĪ»ŹżŹĒ13ČĖ£¬ÖŚŹżŹĒ20ČĖ D. ÖŠĪ»ŹżŹĒ6Š”Ź±£¬ÖŚŹżŹĒ8Š”Ź±
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
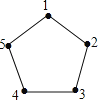
”¾ĢāÄæ”æČēĶ¼£¬Ņ»øöÕżĪå±ßŠĪµÄĪåøö¶„µćŅĄ“Ī±ąŗÅĪŖ![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬“Óijøö¶„µćæŖŹ¼£¬Čō¶„µć±ąŗÅŹĒĘꏿ£¬ŌņŅ»“ĪÄꏱÕė×ß
£¬“Óijøö¶„µćæŖŹ¼£¬Čō¶„µć±ąŗÅŹĒĘꏿ£¬ŌņŅ»“ĪÄꏱÕė×ß![]() øö±ß³¤£»Čō¶„µć±ąŗÅŹĒżŹż£¬ŌņŅ»“ĪĖ³Ź±Õė×ß
øö±ß³¤£»Čō¶„µć±ąŗÅŹĒżŹż£¬ŌņŅ»“ĪĖ³Ź±Õė×ß![]() øö±ß³¤£®Čō“Ó±ąŗÅ
øö±ß³¤£®Čō“Ó±ąŗÅ![]() æŖŹ¼×ߣ¬ŌņµŚ
æŖŹ¼×ߣ¬ŌņµŚ![]() “Īŗó£¬Ėł“¦¶„µć±ąŗÅŹĒ_____________£®
“Īŗó£¬Ėł“¦¶„µć±ąŗÅŹĒ_____________£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ(1)£ØĢ½¾æ£©Čō![]() £¬Ōņ“śŹżŹ½
£¬Ōņ“śŹżŹ½![]()
£ØĄą±Č£©Čō![]() £¬Ōņ
£¬Ōņ![]() µÄÖµĪŖ £»
µÄÖµĪŖ £»
(2)£ØÓ¦ÓĆ£©µ±![]() Ź±£¬“śŹżŹ½
Ź±£¬“śŹżŹ½![]() µÄÖµŹĒ5£¬Ēóµ±
µÄÖµŹĒ5£¬Ēóµ±![]() Ź±£¬
Ź±£¬ ![]() µÄÖµ£»
掙术
(3)£ØĶĘ¹ć£©µ±![]() Ź±£¬“śŹżŹ½
Ź±£¬“śŹżŹ½![]() µÄÖµĪŖ
µÄÖµĪŖ![]() £¬µ±
£¬µ±![]() Ź±£¬
Ź±£¬![]() µÄÖµĪŖ (ŗ¬
µÄÖµĪŖ (ŗ¬![]() µÄŹ½×Ó±ķ)
µÄŹ½×Ó±ķ)
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Õż·½ŠĪABCDÖŠ£Øø÷±ß¶¼ĻąµČ£¬ø÷½Ē¶¼ĪŖÖ±½Ē£©£¬EĪŖÉäĻßBCÉĻŅ»¶Æµć£¬µćB¹ŲÓŚÖ±ĻßAEµÄ¶Ō³ĘµćĪŖ![]() £¬ÉäĻß
£¬ÉäĻß![]() ÓėÉäĻßCDĻą½»ÓŚµćF£®Éč
ÓėÉäĻßCDĻą½»ÓŚµćF£®Éč![]() £¬
£¬![]() £®
£®
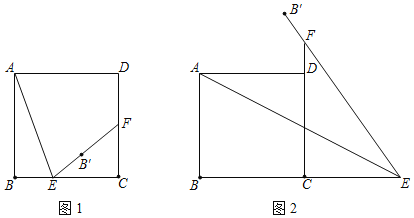
£Ø1£©ČēĶ¼1£¬Õż·½ŠĪABCDµÄ±ß³¤ĪŖ20£¬µ±µćEŌŚ±ßBCÉĻŌĖ¶Æ£ØµćEÓėB”¢C²»ÖŲŗĻ£©Ź±£©£ŗ
¢Ł![]() µÄÖܳ¤Ź¼ÖÕ²»±ä£¬ĒėÄćĒó³öÕāøö²»±äµÄÖµ£»
µÄÖܳ¤Ź¼ÖÕ²»±ä£¬ĒėÄćĒó³öÕāøö²»±äµÄÖµ£»
¢Śµ±![]() Ź±£¬ĒóyµÄÖµ¼°
Ź±£¬ĒóyµÄÖµ¼°![]() µÄĆ껿.
µÄĆ껿.
£Ø2£©ČēĶ¼2£¬µ±µćEŌŚ±ßBCŃÓ³¤ĻßÉĻŹ±£¬
¢Ł²ĀĻėBE”¢EF”¢DFÖ®¼äµÄŹżĮæ¹ŲĻµŹĒ__________.
¢ŚĒóÖ¤£ŗ![]() µÄĆ껿
µÄĆ껿![]() .
.
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com