
【题目】
(1)解方程: ![]() +
+ ![]() =2
=2
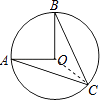
(2)如图,在⊙O中,OA⊥OB,∠A=20°,求∠B的度数.
【答案】
(1)解:去分母得,1﹣(x+2)=2(x﹣2),
去括号得,1﹣x﹣2=2x﹣4,
移项得,﹣x﹣2x=﹣4﹣1+2,
合并同类项得,﹣3x=﹣3,
系数化为1得,x=1,
经检验,x=1是原方程的解
(2)解:连接OC,
∵OA⊥OB,
∴∠AOB=90°,
∴∠ACB=45°.
又∴OA=OC,∠A=20°,
∴∠ACO=20°,
∴∠OCB=25°.
又∵OC=OB
∴∠B=25°.
【解析】(1)先把分式方程化为整式方程,求出x的值,再代入最简公分母进行检验即可;(2)连接OC,先根据圆周角定理求出∠ACB的度数,再由等腰三角形的性质求出∠ACO的度数,进而可得出∠BCO的度数,据此可得出结论.
【考点精析】通过灵活运用去分母法和圆周角定理,掌握先约后乘公分母,整式方程转化出.特殊情况可换元,去掉分母是出路.求得解后要验根,原留增舍别含糊;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半即可以解答此题.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】我们知道![]() ,于是我们说:“
,于是我们说:“![]() 的整数部分为
的整数部分为![]() ,小数部分则可记为
,小数部分则可记为![]() ”.则:
”.则:
(1)![]() 的整数部分为________,小数部分则可记为________;
的整数部分为________,小数部分则可记为________;
(2)已知![]() 的小数部分为
的小数部分为![]() ,
,![]() 的小数部分为
的小数部分为![]() ,那么
,那么![]() 的值是________;
的值是________;
(3)已知![]() 是
是![]() 的整数部分,
的整数部分,![]() 是
是![]() 的小数部分,求
的小数部分,求![]() 的平方根.
的平方根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是AD上一点,延长CE到点F,使∠FBC=∠DCE. 
(1)求证:∠D=∠F;
(2)用直尺和圆规在AD上作出一点P,使△BPC∽△CDP(保留作图的痕迹,不写作法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图抛物线y=ax2+bx+c与x轴交于A、B两点,其中B点坐标为(4,0),直线DE是抛物线的对称轴,且与x轴交于点E,CD⊥DE于D,现有下列结论: ①a<0,②b<0,③b2﹣4ac>0,④AE+CD=4
下列选项中选出的结论完全正确的是( )
A.①②③
B.①②④
C.①③④
D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人用![]() 元购买了
元购买了![]() 套儿童服装,准备以一定价格出售,如果以每套儿童服装
套儿童服装,准备以一定价格出售,如果以每套儿童服装![]() 元的价格为标准,超出的记作正数,不足的记作负数,记录如下:
元的价格为标准,超出的记作正数,不足的记作负数,记录如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:元)
(单位:元)
请你帮他计算出当他卖完这八套儿童服装后,赚了还是赔了,赚(或赔)了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中显示了10名同学平均每周用于阅读课外书的时间和用于看电视的时间(单位:小时)。
(1)用有序实数对表示图中各点。
(2)图中有一个点位于方格的对角线上,这表示什么意思?
(3)图中方格纸的对角线的左上方的点有什么共同的特点?它右下方的点呢?
(4)估计一下你每周用于阅读课外书的时间和用于看电视的时间,在图上描出来,这个点位于什么位置?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com