
分析 分两种情况:①D在AB边上,易得BE=DE=$\frac{1}{2}$BD=2;②D在AC边上,根据角平分线的性质可求BE.
解答 解:分两种情况: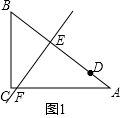 ①D在AB边上,如图1.
①D在AB边上,如图1.
∵将△ABC折叠,使点B落在点D处,折痕交边AB于点E,交另一边于点F,
∴BE=DE=$\frac{1}{2}$BD,
∵AB=5,AD=1,
∴BD=AB-AD=5-1=4,
∴BE=2;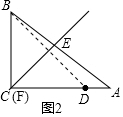 ②D在AC边上,如图2.
②D在AC边上,如图2.
∵在△ABC中,∠C=90°,BC=3,AB=5,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=4,
∵AD=1,
∴CD=3,
∴BC=CD=3,
∵将△ABC折叠,使点B落在点D处,折痕交边AB于点E,交另一边于点F,
∴C与F重合,
∴∠BCE=∠DCE,
∴$\frac{BE}{AE}$=$\frac{BC}{AC}$,
∴$\frac{BE}{5-BE}$=$\frac{3}{4}$,
解得BE=$\frac{15}{7}$.
故答案为2或$\frac{15}{7}$.
点评 本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了勾股定理以及角平分线的性质.进行分类讨论是解题的关键.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:解答题
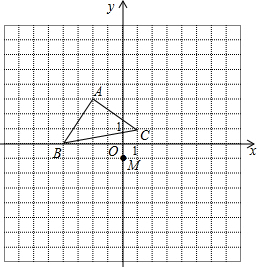 在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,3),B(-4,0),C(1,1).
在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,3),B(-4,0),C(1,1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{8}$ | D. | $\frac{5}{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
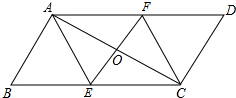 如图,点E,F分别放在?ABCD的边BC、AD上,AC、EF交于点O,请你添加一个条件(只添一个即可),使四边形AECF是平行四边形,你所添加的条件是AF=CE.
如图,点E,F分别放在?ABCD的边BC、AD上,AC、EF交于点O,请你添加一个条件(只添一个即可),使四边形AECF是平行四边形,你所添加的条件是AF=CE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 5 | D. | -5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB为⊙O的直径,点P是⊙O外一点,PD与⊙O相切于点C,与BA的延长线交于点D,DE⊥PO,交PO的延长线于点E,连接PB,∠EDB=∠EPB.
如图,AB为⊙O的直径,点P是⊙O外一点,PD与⊙O相切于点C,与BA的延长线交于点D,DE⊥PO,交PO的延长线于点E,连接PB,∠EDB=∠EPB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com