
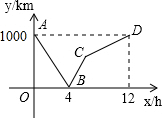
 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),y与x之间的函数关系如图中折线所示,根据图象得到下列结论,其中正确的是( )
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),y与x之间的函数关系如图中折线所示,根据图象得到下列结论,其中正确的是( )| A. | B点表示此时快车到达乙地 | |
| B. | B-C-D段表示慢车先加速后减速最后到达甲地 | |
| C. | 快车的速度为166$\frac{2}{3}$km/h | |
| D. | 慢车的速度为125km/h |
分析 由图象可知点B的纵坐标为0,即两车间距离为0,可判断A;B-C-D段表示快、慢车相遇后行驶一段时间快车到达乙地的情况;由慢车行驶全程1000km用时12h可得慢车速度,即可判断D;根据相遇时两车行驶路程等于甲、乙两地距离,列方程可得快车速度,即可判断C.
解答 解:点B表示两车出发4h后相遇,故A选项错误;
B-C-D段表示快、慢车相遇后行驶一段时间快车到达乙地,慢车继续行驶,慢车共用12h到达甲地,故B选项错误;
由图可知,甲、乙两地相距1000km,慢车行驶全程共用12h到达甲地,
∴慢车的速度为$\frac{1000}{12}$=83$\frac{1}{3}$km/h,故D选项错误;
设快车速度为xkm/h,则4x+4×83$\frac{1}{3}$=1000,
解得:x=166$\frac{2}{3}$,
即快车速度为166$\frac{2}{3}$km/h,故C选项正确;
故选:C.
点评 本题主要考查一次函数的图象与应用,根据题意理解图象上的特殊点的实际意义是解题的关键.


科目:初中数学 来源: 题型:选择题
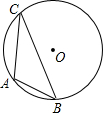 如图,已知⊙O的直径为8cm,A、B、C三点在⊙O上,且∠ACB=30°,则AB长为( )
如图,已知⊙O的直径为8cm,A、B、C三点在⊙O上,且∠ACB=30°,则AB长为( )| A. | 3cm | B. | 4cm | C. | 2$\sqrt{2}$cm | D. | 2$\sqrt{3}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{45}-2\sqrt{5}=\sqrt{5}$ | B. | (π-3.14)0=0 | C. | a2•a5=a10 | D. | (a+b)2=a2+b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,用若干个全等的正五边形可以拼成一个环状,图中所示的是前3个正五边形的拼接情况,要完全拼成一个圆环还需要的正五边形个数是( )
如图,用若干个全等的正五边形可以拼成一个环状,图中所示的是前3个正五边形的拼接情况,要完全拼成一个圆环还需要的正五边形个数是( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
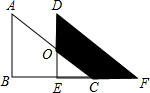 如图,两个全等的直角三角形重叠在一起,将Rt△ABC沿着BC的方向平移到Rt△DEF的位置,已知AB=5,DO=2,平移距离为3,则阴影部分的面积为( )
如图,两个全等的直角三角形重叠在一起,将Rt△ABC沿着BC的方向平移到Rt△DEF的位置,已知AB=5,DO=2,平移距离为3,则阴影部分的面积为( )| A. | 12 | B. | 24 | C. | 21 | D. | 20.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | ||
| C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com