

分析 (1)只要证明Rt△ABE≌Rt△BCF(SAS),即可推出∠BAE=∠CBF,由∠BAE+∠BEA=90°,推出∠CBF+∠BEA=90°,推出∠BGE=90°;
(2)首先证明QF=QB,设PF=k,则PB=2k,在Rt△BPQ中,设BQ=x,可得x2=(x-k)2+4k2,推出x=$\frac{5}{2}$k,根据sin∠BQP=$\frac{BP}{QB}$计算即可.
(3)由GN∥HM,推出△AGN∽△AHN,推出$\frac{{S}_{△AGN}}{{S}_{△AHM}}$=($\frac{AN}{AM}$)2,推出$\frac{{S}_{△AGN}}{1}$=($\frac{2}{\sqrt{5}}$)2,推出S△AGN=$\frac{4}{5}$,根据四边形GHMN的面积=S△AHM-S△AGN计算即可.
解答 (1)证明:如图1中,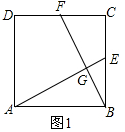
∵E、F分别是正方形ABCD边BC、CD的中点,
∴CF=BE,
在Rt△ABE和Rt△BCF中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABE=∠BCF}\\{BE=CF}\end{array}\right.$,
∴Rt△ABE≌Rt△BCF(SAS),
∴∠BAE=∠CBF,
∵∠BAE+∠BEA=90°,
∴∠CBF+∠BEA=90°,
∴∠BGE=90°,
∴AE⊥BF.
(2)解:如图2中,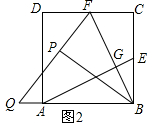
由题意,FP=FC,∠FPB=∠C=90°,
∵CD∥AB,
∴∠CFB=∠ABF,
∴∠ABF=∠PFB,
∴QF=QB,设PF=k,则PB=2k,
在Rt△BPQ中,设BQ=x,
∴x2=(x-k)2+4k2,
∴x=$\frac{5}{2}$k,
∴sin∠BQP=$\frac{BP}{QB}$=$\frac{2k}{\frac{5}{2}k}$=$\frac{4}{5}$.
(3)如图3中,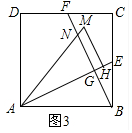
∵正方形ABCD的面积为4,
∴边长为2,
∵∠BAE=∠EAM,AE⊥BF,
∴AN=AB=2,∵∠AHM=90°,
∴GN∥HM,
∴△AGN∽△AHN,
∴$\frac{{S}_{△AGN}}{{S}_{△AHM}}$=($\frac{AN}{AM}$)2,
∴$\frac{{S}_{△AGN}}{1}$=($\frac{2}{\sqrt{5}}$)2,
∴S△AGN=$\frac{4}{5}$,
∴四边形GHMN的面积=S△AHM-S△AGN=1-$\frac{4}{5}$=$\frac{1}{5}$.
点评 本题考查四边形综合题、正方形的性质、翻折变换、全等三角形的判定和性质、相似三角形的判定和性质、锐角三角函数、勾股定理等知识,解题的关键是灵活运用所学知识,学会利用参数解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
 请你根据学函数这一章所获得的学习经验来探究.
请你根据学函数这一章所获得的学习经验来探究.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两点之间线段最短 | |
| B. | 三角形的内心是这个三角形三边垂直平分线的交点 | |
| C. | 对角线互相垂直的四边形是菱形 | |
| D. | 五边形的外角和为540度 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 137×108 | B. | 1.37×109 | C. | 1.37×1010 | D. | 0.137×1011 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 数轴上的每一个点都有一个有理数与它对应 | |
| B. | 如果两条直线被第三条直线所截,那么一对同位角的平分线互相平行 | |
| C. | 如果一个角的两边分别与另一个角的两边平行,那么这两个角一定相等 | |
| D. | 当直线a平行于直线b时,直线a上任取一点到直线b的距离都相等 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com