练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．解方程：$\frac{1}{x-1}$-1=0．

    分析 分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．

    解答 解：去分母得：1-x+1=0，
    解得：x=2，
    经检验x=2是分式方程的解．

    点评 此题考查了解分式方程，利用了转化的思想，解分式方程注意要检验．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    17．计算：（π-$\sqrt{5}$）0+$\root{3}{27}$+（-1）2016-$\sqrt{3}$•tan60°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

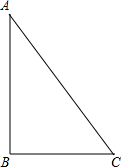    18．如图，在Rt△ABC中，∠ABC=90°，
    （1）①作∠BCA的平分线，交AB于点O（用尺规作图法，保留作图痕迹，不要求写作法）．
            ②以O为圆心，OB为半径作圆．
    （2）在你所作的图中，AC与⊙O的位置关系是相切
    （3）在（1）的条件下，若BC=6，AB=8，求⊙O的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．郑州市初中毕业生体育测试项目有四项，其中“长跑”为必测项目，从“50米跑”或“一分钟跳绳”中选一项测试；从“立定跳远”或“实心球”中选一项测试；从“篮球”或“足球”中选一项测试．已知小亮、小明均选择“篮球”，则两人四个测试项目均相同的概率是$\frac{1}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．计算：$\sqrt{8}$-2sin45°+（2017-π）0-（$\frac{1}{3}$）-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

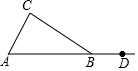    12． 如图，在△ABC中，AB=BC，点D在AB的延长线上．
    （1）用尺规按下列要求作图，并在图中标明相应的字母（保留作图痕迹，不写作法）．
    ①作∠CBD的平分线BM；
    ②作边BC上的中线AE，并延长AE交BM于点F．
    （2）求证：BF∥AC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

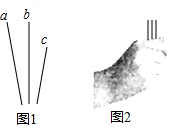    19．甲、乙、丙三人用三根完全相同的吸管玩游戏，将其中一根剪去一段（如图1所示），甲把三根吸管按如图2所示的方式拿在手中，使露出的部分完全相同，乙先从中抽取一根不放回，丙再从中抽取一根．
    （1）乙抽到吸管c的概率为$\frac{1}{3}$；
    （2）用画树状图或列表的方法，求乙、丙两人都没有抽到吸管c的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

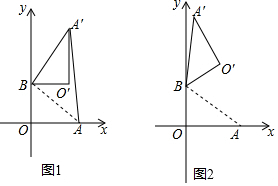    16．在平面直角坐标系中，O为原点，B（0，6），A（8，0），以点B为旋转中心把△ABO逆时针旋转，得△A′BO′，点O，A旋转后的对应点为O′，A′，记旋转角为β．
    （1）如图1，若β=90°，求AA′的长；
    （2）如图2，若β=120°，求点O′的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．（1）请在横线上填写合适的内容，完成下面的证明：
    如图①，如果AB∥CD，求证：∠APC=∠A+∠C．
    证明：过P作PM∥AB．
    ∴∠A=∠APM，（两直线平行，内错角相等）
    ∵PM∥AB，AB∥CD（已知）
    ∴PM∥CD，（平行于同一直线的两直线平行）
    ∴∠C=∠CPM（两直线平行，内错角相等）
    ∵∠APC=∠APM+∠CPM，
    ∴∠APC=∠A+∠C（等量代换）
    （2）如图②，AB∥CD，直接写出∠A+∠P+∠Q+∠C=540°．
    （3）如图③，AB∥CD，若∠ABP=x，∠BPQ=y，∠PQC=z，∠QCD=m，你能用x，y，z表示m的大小吗？试说明理由．

    查看答案和解析>>

    同步练习册答案