
【题目】甲骑摩托车从 ![]() 地去
地去 ![]() 地,乙开汽车从
地,乙开汽车从 ![]() 地去
地去 ![]() 地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为
地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为 ![]() (单位:千米),甲行驶的时间为
(单位:千米),甲行驶的时间为 ![]() (单位:小时),
(单位:小时), ![]() 与
与 ![]() 之间的函数关系如图所示,有下列结论:
之间的函数关系如图所示,有下列结论:
①出发1小时时,甲、乙在途中相遇;
②出发1.5小时时,乙比甲多行驶了60千米;
③出发3小时时,甲、乙同时到达终点;
④甲的速度是乙速度的一半.
其中,正确结论的个数是( )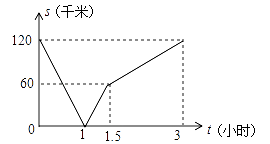
A.4
B.3
C.2
D.1
【答案】B
【解析】解:由图象可得:出发1小时,甲、乙在途中相遇,故①正确;
甲骑摩托车的速度为:120÷3=40(千米/小时),设乙开汽车的速度为a千米/小时,
则12040+a=1,
解得:a=80,
∴乙开汽车的速度为80千米/小时,
∴甲的速度是乙速度的一半,故④正确;
∴出发1.5小时,乙比甲多行驶了:1.5×(8040)=60(千米),故②正确;
乙到达终点所用的时间为1.5小时,甲得到终点所用的时间为3小时,故③错误;
∴正确的有3个,
故选:B.
【考点精析】掌握函数的图象是解答本题的根本,需要知道函数的图像是由直角坐标系中的一系列点组成;图像上每一点坐标(x,y)代表了函数的一对对应值,他的横坐标x表示自变量的某个值,纵坐标y表示与它对应的函数值.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】阅读材料:
材料1、若一元二次方程ax2+bx+c=0(a≠0)的两根为x1 , x2 , 则x1+x2=![]() , x1x2=
, x1x2=![]() .
.
材料2、已知实数m、n满足m2﹣m﹣1=0,n2﹣n﹣1=0,且m≠n,求![]() 的值.
的值.
解:由题知m、n是方程x2﹣x﹣1=0的两个不相等的实数根,根据材料1得
m+n=1,mn=﹣1
∴![]() =
=![]()
根据上述材料解决下面问题:
(1)一元二次方程2x2+3x﹣1=0的两根为x1、x2 , 则x1+x2= , x1x2= .
(2)已知实数m、n满足2m2﹣2m﹣1=0,2n2﹣2n﹣1=0,且m≠n,求m2n+mn2的值.
(3)已知实数p、q满足p2=3p+2,2q2=3q+1,且p≠2q,求p2+4q2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区超市第一次用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的 ![]() 倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价-进价)
倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价-进价)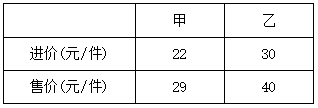
(1)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该超市第二次以第一次的进价又购进甲、乙两种商品.其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售.第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元,求第二次乙种商品是按原价打几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中添加下列条件,不能判定四边形ABCD是菱形的是( )
A. AB=BC B. AC⊥BD C. AC=BD D. ∠ABD=∠CBD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:一次函数 ![]() 的图象与反比例函数
的图象与反比例函数 ![]() 的图象交于M、N两点
的图象交于M、N两点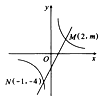
(1)求反比例函数和一次函数的关系式
(2)根据图象写出使反比例函数的值大于一次函数的值的x的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com