
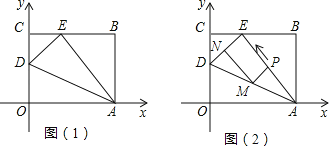
����Ŀ����ͼ��1����OABC��һ�ŷ���ƽ��ֱ������ϵ�еľ���ֽƬ��OΪ����ԭ�㣬��A��x����������ϣ���C��y����������ϣ�OA=5��OC=4����OC����ȡһ��D������ֽƬ��AD��ת��ʹ��O����BC���ϵĵ�E����
��1����ֱ��д��D��E��������ꣻ
��2����ͼ��2�����߶�AE����һ����P������A��E�غϣ����Ե�A��AE�����������˶����˶����ٶ�Ϊÿ��1����λ���ȣ����˶�ʱ��Ϊt�룬����P��ED��ƽ���߽�AD�ڵ�M������M��AEƽ���߽�DE�ڵ�N�����ı���PMNE�����S��ʱ��t֮��ĺ�����ϵʽ��
��3���ڣ�2���������£���tΪ��ֵʱ����A��M��EΪ������������ǵ��������Σ�
���𰸡���1����0��![]() ����2��S����PMNE= -
����2��S����PMNE= -![]() t2+
t2+![]() t��3��t=
t��3��t=![]() ��t=2
��t=2![]() ʱ����A��M��EΪ�����������Ϊ����������
ʱ����A��M��EΪ�����������Ϊ����������
��������
��1���ȸ��ݹ��ɶ������BE�ij��������ɵó�CE�ij������E�����꣬���ù��ɶ��������OD���ɣ�
��2�����жϳ���APM�ס�AED����ʾ��PM�������![]() ȷ������ֵ��
ȷ������ֵ��
��3���������������������AEΪ���������εĵף���ME=MA��������λ�����M�����꣬����������AEΪ���������ε�������AM=AE=5�����ù��ɶ���������������������ɣ�
��1���������֪���ۺ�AD���ı���OAED�ĶԳ��ᣬ
����Rt��ABE��AE=AO=5��AB=4��
BE= ![]() ��
��
��CE=2��
��E��������2��4����
��Rt��DCE��DC2+CE2=DE2��
�֡�DE=OD��
�ࣨ4��OD��2+22=OD2��
��ã�OD= ![]() ��
��
��D��������0��![]() ����
����
��2����PM��ED��
���APM�ס�AED��
��![]() ��
��
��AP=t��ED= ![]() ��AE=5��
��AE=5��
PM= ![]() ��
��![]() =
=![]() ��
��
��PE=5��t��
���ı���PMNEΪ���Σ�
��S����PMNE=PM��PE=![]() ����5��t��=-
����5��t��=-![]() ��
��
��3������������AEΪ���������εĵף���ME=MA����ͼ1��

��Rt��AED��ME=MA��
��PM��AE��
��PΪAE���е㣬
��t=AP=![]() AE=
AE=![]() ��
��
�֡�PM��ED��
��MΪAD���е㣮
����M��MF��OA������ΪF����MF����OAD����λ�ߣ�
��MF=![]() OD=
OD=![]() ��OF=
��OF=![]() OA=
OA=![]() ��
��
�൱t=![]() ʱ����0��
ʱ����0��![]() ��5������AMEΪ���������Σ�
��5������AME����������
����������AEΪ���������ε�������AM=AE=5����ͼ1��
��Rt��AOD��AD=![]() ��
��
����M��MF��OA������ΪF��
��PM��ED��
���APM�ס�AED��
��![]()
��t=AP=![]() ��
��
��PM=![]() t=
t=![]() ��
��
��t=2![]() ʱ����0��2
ʱ����0��2![]() ��5��
��5��
�ۺϣ���������֪��t=![]() ��t=2
��t=2![]() ʱ����A��M��EΪ�����������Ϊ���������Σ�
ʱ����A��M��EΪ�����������Ϊ���������Σ�


 ̽���빮�̺��Ͽ�ѧ����������ϵ�д�
̽���빮�̺��Ͽ�ѧ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������£�С����������ͼ���߶�AB��ʾ�����ڵ����ϵ�Ӱ����ͼ���߶�BC��ʾ���߶�DE��ʾ��˵ĸߣ��߶�FG��ʾһ�¸�ǽ��
��1��������ͼ�л��������ͬһʱ�������������γɵ�Ӱ�ӣ������߶α�ʾ��
��2�����С��������AB=1.6m������Ӱ��BC=2.4m����˵ĸ�DE=15m��������ǽ�ľ���EG=16m���������˵�Ӱ������ǽ�ϵij��ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
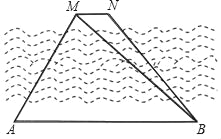
����Ŀ����ͼ����һ���ӵı���������Ŀ��M��N������λ�����Ķ��趨�����۲��A��B����֪AB��MN����A���á�MAB��60�㣬��B���á�MBA��45�㣬AB��600�ף�
(1)���M��AB�ľ��룻������������ţ�
(2)��B���ֲ�á�NBA��53�㣬��MN�ij����������ȷ��1�ף�
���ο����ݣ�![]() ��1.732��sin53���0.8��cos53���0.6��tan53���1.33��cot53���0.75��
��1.732��sin53���0.8��cos53���0.6��tan53���1.33��cot53���0.75��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
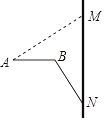
����Ŀ�����������ǵij��д����˼���ķ��㣮��ͼ������г���������г����κ����С��������ʱ��С�����֧�ܵĵ�N�����涥��M�ľ���MN=75cm���ҿ��Կ�������洹ֱ��չ��С����ʹ���汣��ˮƽ��AB��MN����MAB=��MNB=37������֧�ܳ�BN�������AB�ij���֮�͵���MN�ij��ȣ���С��������Ŀ���AB�������ȷ��1cm���ο����ݣ�sin37���0.6��cos37���0.8��tan37���0.75��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������״�ʹ�С��ȫ��ͬ�ķ���ֽ������ֽ��ÿ��С�����εı߳���Ϊ1���߶�AC�������˵����С�����εĶ�����

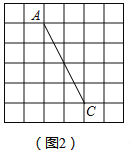
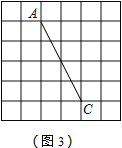
��1����ͼ��1���У���P��С�����εĶ����ϣ�������P����ֱ��AC�ĶԳƵ�Q
��2����ͼ��2���У�����һ�����߶�ACΪ�Խ��ߡ����Ϊ6�ľ���ABCD���ҵ�B�͵�D����С�����εĶ�����
��3����ͼ��3���У�B��AC���е㣬���߶�AB�Ĵ�ֱƽ���ߣ�Ҫ�ٽ����̶�ֱ�ߣ��Ҳ�����ֱ���е�ֱ�ǣ��ڱ�����Ҫ����ͼ�ۼ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
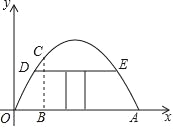
����Ŀ����һ�����������߲˴��������������ͼ��ʾ��ƽ��ֱ������ϵ�У������߿����ú���y��ax2+bx����ʾ����֪OA��8�ף�����O��2�״������BCΪ![]() �ף�
�ף�
��1����������ߵĽ���ʽ��
��2������������DE��DE��OA����һ���ţ�Ҫ���ŵĸ߶�Ϊ1.5�ף������DE�ij����Ƕ����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2+��2m��1��x+m2=0������ʵ����x1��x2��
��1����ʵ��m��ȡֵ��Χ��
��2����x12��x22=0ʱ����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
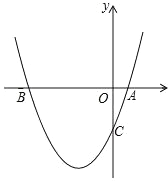
����Ŀ����ͼ����֪���κ��� y��x2+bx+c ���� A��1��0����C��0����3��
��1����˶��κ����Ľ���ʽ��
��2�����ABC �������
��3�����������ϴ���һ�� P ʹ��ABP �����Ϊ 10��������� P �����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��Ͷ������һ�ֽ���Ϊÿ��20Ԫ�Ļ���̨�ƣ����۹����з��֣�ÿ��������y�����������۵���x��Ԫ��֮��Ĺ�ϵ�ɽ��ƵĿ���һ�κ�����y=��10x+500�������۹��������۵��۲����ڳɱ��ۣ���ÿ���������ڳɱ��۵�60%��
��1����С��ÿ�»������Ϊw��Ԫ������ÿ�»������w��Ԫ�������۵���x��Ԫ��֮��ĺ�����ϵʽ����ȷ���Ա���x��ȡֵ��Χ��
��2�������۵��۶�Ϊ����Ԫʱ��ÿ�¿ɻ���������ÿ�µ���������Ƕ��٣�
��3�����С����Ҫÿ�»�õ�������2000Ԫ����ôС��ÿ�µijɱ�������Ҫ����Ԫ�����ɱ�=��������������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com