
分析 先通分、化简,然后代入求值.
解答 解:$\frac{1}{a+b}+\frac{1}{b}+\frac{b}{a(a+b)}$,
=$\frac{ab+a(a+b)+{b}^{2}}{ab(a+b)}$,
=$\frac{(a+b)^{2}}{ab(a+b)}$,
=$\frac{a+b}{ab}$.
∵a=$\frac{\sqrt{5}+1}{2}$,b=$\frac{\sqrt{5}-1}{2}$,
∴ab=$\frac{\sqrt{5}+1}{2}$•$\frac{\sqrt{5}-1}{2}$=$\frac{(\sqrt{5})^{2}-1}{{2}^{2}}$=1,
a+b=$\frac{\sqrt{5}+1+\sqrt{5}-1}{2}$=$\sqrt{5}$,
∴$\frac{a+b}{ab}$=$\frac{\sqrt{5}}{1}$=$\sqrt{5}$.即:$\frac{1}{a+b}+\frac{1}{b}+\frac{b}{a(a+b)}$=$\sqrt{5}$.
点评 本题考查了分式的化简求值.解答此题的关键是把分式化到最简,然后代值计算.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | $\frac{11}{3}$ | D. | -2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
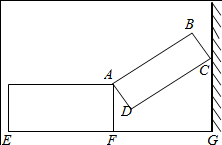 如图,一种侧面形状为矩形的行李箱,箱盖打开后,盖子的一端靠在墙上,此时BC=10cm,箱底端点E与墙角G的距离为65cm,∠DCG=60°.
如图,一种侧面形状为矩形的行李箱,箱盖打开后,盖子的一端靠在墙上,此时BC=10cm,箱底端点E与墙角G的距离为65cm,∠DCG=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
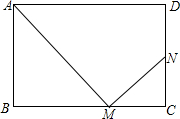 在矩形ABCD中,AB=a,AD=b,点M为BC边上一动点(点M与点B、C不重合),连接AM,过点M作MN⊥AM,垂足为M,MN交CD或CD的延长线于点N.
在矩形ABCD中,AB=a,AD=b,点M为BC边上一动点(点M与点B、C不重合),连接AM,过点M作MN⊥AM,垂足为M,MN交CD或CD的延长线于点N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com